如图，在△ABC中，∠ACB=90°，AC=BC=1，E，F是线段AB上的两个动点，且∠ECF=45°，过点E，F分别作BC，AC的垂线相交于点M，垂足分别为H，G．下列判断：①AB=2；②当点E与点B重合时，MH=12；③AEBC=ACB

Question

如图，在△ABC中，∠ACB=90°，AC=BC=1，E，F是线段AB上的两个动点，且∠ECF=
45°，过点E，F分别作BC，AC的垂线相交于点M，垂足分别为H，G．下列判断：
①AB=

√(2)；②当点E与点B重合时，MH=(1)/(2)；③(AE)/(BC)=(AC)/(BF)；④AF+BE=EF．
其中正确的结论有（　　）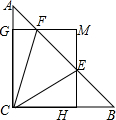

A. ①②③

B. ①③④

C. ①②④

D. ①②③④

Answer 1

①由题意知，△ABC是等腰直角三角形，
则AB=√(AC2+BC2)=√(2)，故①正确；
②如图1，当点E与点B重合时，点H与点B重合，

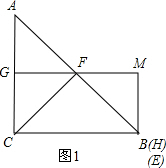
∴MB⊥BC，∠MBC=90°，
∵MG⊥AC，
∴∠MGC=90°=∠C=∠MBC，
∴MG∥BC，四边形MGCB是矩形，
∴MH=MB=CG，
∵∠FCE=45°=∠ABC，∠A=∠ACF=45°，
∴CF=AF=BF，
∴FG是△ACB的中位线，
∴GC=(1)/(2)AC=MH，故②正确；
④如图2所示，

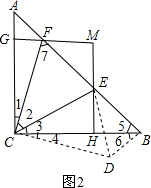
∵AC=BC，∠ACB=90°，
∴∠A=∠5=45°．
将△ACF顺时针旋转90°至△BCD，
则CF=CD，∠1=∠4，∠A=∠6=45°；BD=AF；
∵∠2=45°，
∴∠1+∠3=∠3+∠4=45°，
∴∠DCE=∠2．
在△ECF和△ECD中，

CF=CD

∠2=∠DCE

CE=CE

，
∴△ECF≌△ECD（SAS），
∴EF=DE．
∵∠5=45°，
∴∠DBE=90°，
∴DE²=BD²+BE²，即EF²=AF²+BE²，故④错误；
③∵∠7=∠1+∠A=∠1+45°=∠1+∠2=∠ACE，
∵∠A=∠5=45°，
∴△ACE∽△BFC，
∴(AE)/(BC)=(AC)/(BF)；
故③正确．
故选A．