（文科做）（本题满分14分）如图，在长方体ABCD—A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动.（1）证明：D1E⊥A1D;（2）当E为AB的中点时，求点E到面ACD1

Question

（文科做）（本题满分14分）如图，在长方体
ABCD — A ₁ B ₁ C ₁ D ₁ 中， AD=AA ₁ = 1， AB= 2，点E在棱 AB 上移动.
（1）证明： D ₁ E ⊥ A ₁ D ;
（2）当 E 为 AB 的中点时，求点 E 到面 ACD ₁ 的距离；
（3） AE 等于何值时，二面角 D ₁ — EC － D 的大小为 .　　　　　　　　　　　　　　　　　　　　　　

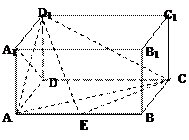
（理科做）(本题满分14分)
如图，在直三棱柱 ABC – A ₁ B ₁ C ₁ 中，∠ ACB = 90°， CB = 1，
CA =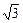 ， AA ₁ = ， M 为侧棱 CC ₁ 上一点， AM ⊥ BA ₁ ．
（Ⅰ）求证： AM ⊥平面 A ₁ BC ；
（Ⅱ）求二面角 B – AM – C 的大小；
（Ⅲ）求点 C 到平面 ABM 的距离．

Answer 1

、（文）解法一（1）∵AE⊥平面AA1DD1，A1D⊥AD1，∴D1E⊥A1D．（2）设点E到面ACD1的距离为h，在△ACD1中，AC=CD1=，AD1=，故（3）过D作DH⊥CE于H，连D1H、DE，则D1H⊥CE，∴∠DHD1为二面角D1—EC—D的平面角.设AE=x，则BE=2－x， （3）设平面D1EC的法向量，由 令b="1 " ∴c=2 a=2－x，∴依题意∴（不合，舍去），∴AE=时，二面角D1—EC—D的大小为.  （Ⅲ）设点C到平面ABM的距离为h，易知BO =，可知S△ABM =· AM · BO =×   ∵VC – ABM = VM – ABC  ∴hS△ABM =MC ·S△ABC  ∴h =  ∴点C到平面ABM的距离为解法二：（Ⅰ）同解法一（Ⅱ）如图以C为原点，CA，CB，CC1所在直线  分别为x轴，y轴，z轴，建立空间直角坐标系，则A (，0，0)，A1(，0，)，B (0，1，0)，设M (0，0，z1)     ∵AM⊥BA1．∴，即– 3 + 0 +z1 = 0，故z1 =，所以M (0，0，)    设向量m = (x，y，z)为平面AMB的法向量，则m⊥，m⊥，则即，令x = 1，平面AMB的一个法向量为m = (1，，)，显然向量是平面AMC的一个法向量cos < m，，易知，m与所夹的角等于二面角B—AM—C的大小，故所求二面角的大小为45°．（Ⅲ）所求距离为：，  即点C到平面ABM的距离为 解析