如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（-1，0），与y轴的交点B在（0，-2）和（0，-1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc>0②4a+2b+c>0③4ac-b2<8

Question

如图，已知二次函数y=ax²+bx+c（a≠0）的图象与x轴交于点A（-1，0），与y轴的交点B在（0，-2）和（0，-1）之间（不包括这两点），对称轴为直线x=1．下列结论：
①abc>0
②4a+2b+c>0
③4ac-b²<8a
④

(1)/(3)<a<(2)/(3) 
⑤b>c．
其中含所有正确结论的选项是（　　）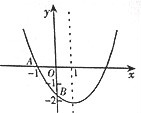

A. ①③

B. ①③④

C. ②④⑤

D. ①③④⑤

Answer 1

①∵函数开口方向向上，
∴a>0；
∵对称轴在原点左侧
∴ab异号，
∵抛物线与y轴交点在y轴负半轴，
∴c<0，
∴abc>0，
故①正确；
②∵图象与x轴交于点A（-1，0），对称轴为直线x=-1，
∴图象与x轴的另一个交点为（3，0），
∴当x=2时，y<0，
∴4a+2b+c<0，
故②错误；
③∵图象与x轴交于点A（-1，0），
∴当x=-1时，y=（-1）²a+b×（-1）+c=0，
∴a-b+c=0，即a=b-c，c=b-a，
∵对称轴为直线x=1
∴-(b)/(2a)=1，即b=-2a，
∴c=b-a=（-2a）-a=-3a，
∴4ac-b²=4•a•（-3a）-（-2a）²=-16a²<0
∵8a>0
∴4ac-b²<8a
故③正确
④∵图象与y轴的交点B在（0，-2）和（0，-1）之间，
∴-2<c<-1
∴-2<-3a<-1，
∴(2)/(3)>a>(1)/(3)；
故④正确
⑤∵a>0，
∴b-c>0，即b>c；
故⑤正确；
故选：D．