早教吧作业答案频道 -->数学-->
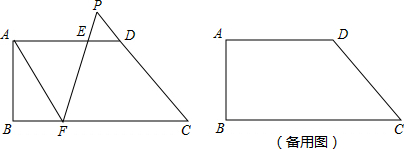
如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=4,BC=9,AD=6,点E,F分别在边AD,BC上,且BF=2DE,联结FE,FE的延长线于CD的延长线相交于点P,设DE=x,PEEF=y.(1)求y关于x的函数解析式,并写出函数的
题目详情
如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=4,BC=9,AD=6,点E,F分别在边AD,BC上,且BF=2DE,联结FE,FE的延长线于CD的延长线相交于点P,设DE=x,
=y.
(1)求y关于x的函数解析式,并写出函数的定义域;
(2)当以ED为半径的 E与以FB为半径的 F外切时,求x的值;
(3)当△AEF∽△PED时,求x的值.
| PE |
| EF |
(1)求y关于x的函数解析式,并写出函数的定义域;
(2)当以ED为半径的 E与以FB为半径的 F外切时,求x的值;
(3)当△AEF∽△PED时,求x的值.

▼优质解答
答案和解析
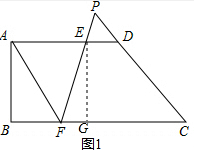 (1)∵BF=2DE,DE=x,
(1)∵BF=2DE,DE=x,
∴BF=2x,
∵BC=9,
∴CF=9-2x,
∵AD∥BC,
∴△PDE∽△PCF,
∴
=
,
∵
=y,
∴y=
=
,
∴y=
(0<x<3);
(2)∵ E的半径=x, F的半径=2x,
∵以ED为半径的 E与以FB为半径的 F外切,
∴x+2x=EF,
过E作EG⊥BC于G,
∴EG=AB=4,FG=6-3x,
∴EF=
=
,
∴x+2x=
,
解得x=
;
(3)当△AEF∽△PED时,
①当∠EAF=∠EDP时,有
=
,
即
=
,
解得:x=
;
②当∠EFA=∠EDP时,过E作EG∥PC交BC于G,
则CG=ED=x,EG=9-3x,
∵△EFA∽△FGE,
∴
=
,
∴EF2=FG•EA,即42+(6-3x)2=(9-3x)(6-x),
∴x=
.
 (1)∵BF=2DE,DE=x,
(1)∵BF=2DE,DE=x,∴BF=2x,
∵BC=9,
∴CF=9-2x,
∵AD∥BC,
∴△PDE∽△PCF,
∴
| PE |
| PF |
| DE |
| CF |
∵
| PE |
| EF |

∴y=
| DE |
| CF-DE |
| x |
| 9-3x |
∴y=
| x |
| 9-3x |
(2)∵ E的半径=x, F的半径=2x,
∵以ED为半径的 E与以FB为半径的 F外切,
∴x+2x=EF,
过E作EG⊥BC于G,
∴EG=AB=4,FG=6-3x,
∴EF=
| EG2+FG2 |
| 42+(6-3x)2 |
∴x+2x=
| 42+(6-3x)2 |
解得x=
| 13 |
| 9 |
(3)当△AEF∽△PED时,
①当∠EAF=∠EDP时,有
| DE |
| EA |
| PE |
| EF |
即
| x |
| 6-x |
| x |
| 9-3x |
解得:x=
| 3 |
| 2 |
②当∠EFA=∠EDP时,过E作EG∥PC交BC于G,
则CG=ED=x,EG=9-3x,
∵△EFA∽△FGE,
∴
| EF |
| FG |
| EA |
| FE |
∴EF2=FG•EA,即42+(6-3x)2=(9-3x)(6-x),
∴x=
9+
| ||
| 12 |
看了如图,在梯形ABCD中,AD∥...的网友还看了以下:
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
设a.b.c分别是三角形ABC的三个内角A.B.C所对的边,由a2=b(b+c)知与满足的关系为 2020-05-15 …
如图正方形被一条曲线分成A、B两部分,下面()说法正确.A.如果a>b,那么A周长大于B周长B.如 2020-05-17 …
已知f(X)=Lg1-X/1+X,a,b属于(-1,1)求证:f(a)+f(B)=F(A+B)/1 2020-05-22 …
a^3+b^3+c^3-3abc=0=(a+b)^3+c^3-3a^2b-3ab^2-3abc,我 2020-07-31 …
已知1/m-1/n=1,求5m+7mn-5n/2n-3mn-2m的值计算(2)a/b-b/a-a^2 2020-11-01 …
下列命题:①a⊥αb⊂α⇒a⊥b;②a⊥αa∥b⇒b⊥α;③a⊥bb⊂α⇒a⊥α;④a⊥αb∥α⇒b 2020-11-02 …
若a(a-1)-(a^2-b)=7,则a^2+b^2)/2-ab=?若a(a-1)-(a²-b)=7 2020-11-07 …
阅读下列例题例ab=1,试求代数式a/(a+1)+b/(b+1)的值因为ab=1,所以a/a+1=a 2020-11-28 …
下列对应f:A→B是从集合A到集合B的函数的是A.A=R,B={x∈r|x>0},f:x→|x|,f 2021-01-01 …