早教吧作业答案频道 -->数学-->
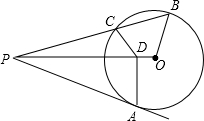
如图,已知PA为O的切线,割线PB交圆于B,C两点,连PO,AD⊥PO于D点,连接CD,BO,求证:∠PDC=∠PBO.
题目详情
如图,已知PA为 O的切线,割线PB交圆于B,C两点,连PO,AD⊥PO于D点,连接CD,BO,求证:∠PDC=∠PBO.

▼优质解答
答案和解析
证明:连结OA,如图,
∵PA为 O的切线,
∴OA⊥AP,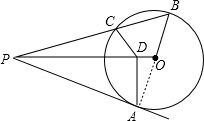
∴∠OAP=90°,
∵AD⊥OP,
∴∠PDA=90°,
而∠DPA=∠APO,
∴△PDA∽△PAO,
∴
=
,
∴PA2=PD•PO,
∵PA为切线,AB为割线,
∴PA2=PC•PB,
∴PD•PO=PC•PB,
即
=
,
而∠DPC=∠BPO,
∴△PCD∽△POB,
∴∠PDC=∠PBO.
∵PA为 O的切线,
∴OA⊥AP,

∴∠OAP=90°,
∵AD⊥OP,
∴∠PDA=90°,
而∠DPA=∠APO,
∴△PDA∽△PAO,
∴
| PA |
| PO |
| PD |
| PA |
∴PA2=PD•PO,
∵PA为切线,AB为割线,
∴PA2=PC•PB,
∴PD•PO=PC•PB,
即
| PC |
| PO |
| PD |
| PB |
而∠DPC=∠BPO,
∴△PCD∽△POB,
∴∠PDC=∠PBO.
看了如图,已知PA为O的切线,割线...的网友还看了以下:
设服从二项分布B~(n,p)的随机变量ξ的期望和方差分别是2.4与1.44,则二项分布的参数n、p 2020-05-15 …
已知命题P:存在m属于R,m+1<=0,命题q:对于任意x属于R,x2+mx+1>0恒成立.若p∩ 2020-05-17 …
点P是矩形ABCD的边AD上的一个动点,矩形的两条边长AB、BC分别为8和15,求点P到矩形的两条 2020-05-20 …
一弹簧秤的称盘质量M1=1.5Kg,盘内放一物体P,P的质量M2=10.5Kg.弹簧质量不计.其劲 2020-06-30 …
当P和3个P连乘+5都是质数时,5个P连乘+5=?注意:3个P连乘也就是大家说的P的3次方。 2020-07-14 …
一个C指针问题#include#defineN10int*fun(inta[N],intn){in 2020-07-23 …
经过下列语句intj,a[10],*p;定义后,下列语句合法的是()A.p=p+2B.p=经过下列语 2020-11-06 …
求你们了!真的不会!谁会,大大地有赏设f(x)=x^2+px+q,g(x)=x^2+qx+p,p、q 2020-12-31 …
写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的命题,并指出所构成的这些命题的真假.(1 2021-01-01 …
(1)P为直线a外一点,在a上取两个点时,在a上有1条线段,与点P能连成1个三角形;取3个点时,在a 2021-01-11 …