早教吧作业答案频道 -->数学-->
某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90天的销售单价p(元/kg)与时间t(天)之间的相关信息如下图,销售量y(kg)与时间t(天)之间满足一次函数关系,
题目详情
某公司购进一种商品的成本为30元/kg,经市场调研发现,这种商品在未来90
天的销售单价p(元/kg)与时间t(天)之间的相关信息如下图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如下表.设第t天的销售利润为w(元)
(1)分别求出售单价p(元/kg)、销售量y(kg)与时间t(天)之间的函数关系式;
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)在实际销售的前50天中,公司决定每销售1kg该商品就捐赠n元利润(n<12)给“精准扶贫”对象.现发现:在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
天的销售单价p(元/kg)与时间t(天)之间的相关信息如下图,销售量y(kg)与时间t(天)之间满足一次函数关系,且对应数据如下表.设第t天的销售利润为w(元)
| 时间t(天) | 10 | 30 |
| 每天的销售量 y(kg) | 180 | 140 |
(2)问:销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)在实际销售的前50天中,公司决定每销售1kg该商品就捐赠n元利润(n<12)给“精准扶贫”对象.现发现:在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.

▼优质解答
答案和解析
(1)设y=kt+b,把t=10,y=180;t=30,y=140代入得到:
,
解得:
,
∴y=-2t+200.
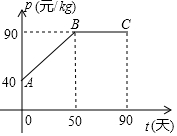
当0<t<50时,设p=kt+40,由图象得B(50,90)
∴50k+40=90,
∴k=1,
∴p=t+40,
当50≤t≤90时,p=90;
(2)由题意可得:w=(-2t+200)(t+40-30)
=-2t2+180t+2000
=-2(t-45)2+6050,
∴t=45时,w最大值为6050元,
w=(-2t+120)(90-30)=-120t+12000,
∵-120<0,
∴w随x增大而减小,
∴t=50时,w最大值=6000,
综上所述第45天利润最大,最大利润为6050元;
(3)设前50天每天扣除捐赠后的日销售利润为m元.
由题意m=-2t2+180t+2000-(-2t+200)n
=-2t2+(180+2n)t+2000-200n,
∵在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴-
=-
≥50,
∴n≥10.
又∵n<12,
∴n的取值范围为:10≤n<12.
|
解得:
|
∴y=-2t+200.
当0<t<50时,设p=kt+40,由图象得B(50,90)
∴50k+40=90,
∴k=1,
∴p=t+40,
当50≤t≤90时,p=90;
(2)由题意可得:w=(-2t+200)(t+40-30)
=-2t2+180t+2000
=-2(t-45)2+6050,
∴t=45时,w最大值为6050元,
w=(-2t+120)(90-30)=-120t+12000,
∵-120<0,
∴w随x增大而减小,
∴t=50时,w最大值=6000,
综上所述第45天利润最大,最大利润为6050元;
(3)设前50天每天扣除捐赠后的日销售利润为m元.
由题意m=-2t2+180t+2000-(-2t+200)n
=-2t2+(180+2n)t+2000-200n,
∵在前50天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,
∴-
| b |
| 2a |
| 180+2n |
| -4 |
∴n≥10.
又∵n<12,
∴n的取值范围为:10≤n<12.
看了某公司购进一种商品的成本为30...的网友还看了以下:
已知函数y=xInx(1)求这个函数的导数(2)求这个函数的图像在点x=1处的切线方程(1)y'= 2020-05-14 …
x+y=(x+y)*1=(x+y)*(1/x+9/y)=1+9+y/x+9x/y=10+y/x+9 2020-05-20 …
if((x=y)=0)这个语句为什么和if(x==y)相等啊?今天看C陷阱与缺陷看到的。if((x 2020-05-23 …
4、已知一次函数y=kx+b的自变量x的取值范围是-1≤x≤5,相对应的函数值范围为-6≤y≤0, 2020-06-06 …
多元回归方程求偏导数?本人对数学一窍不通,如题:多元回归方程为:Y=0.5+0.001X1+0.0 2020-06-29 …
设某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示x与y具有线性相关关 2020-07-19 …
(快~~急!)高二双曲线问题,高手来1.已知双曲线x^2/8-y^2/b^2=1的右焦点为点F,若 2020-07-30 …
(求真理)已知原命题为“x²+y²=0,则x=y=0”.已知原命题为“x²+y²=0,则x=y=0 2020-08-01 …
设随机变量X与Y相互独立,X的概率分布为PX=i=1/3,i=-1,0,1,Y的概率密度为:y∈0, 2020-10-30 …
设随机变量x的分布律为P{x=-1}=1/4,p{x=0}=1/4,p{x=1}=1/2.Y的分布律 2020-10-31 …