早教吧作业答案频道 -->数学-->
设a∈R,把三阶行列式中第一行第二列元素的余子式记为f(x),且关于x的不等式f(x)<0的解集为(-2,0).各项均为正数的数列{an}的前n项和为Sn,点列(an,Sn)(n∈N*)在函数y=f(x)
题目详情
设a∈R,把三阶行列式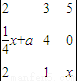 中第一行第二列元素的余子式记为f(x),且关于x的不等式f(x)<0的解集为(-2,0).各项均为正数的数列{an}的前n项和为Sn,点列(an,Sn)(n∈N*)在函数y=f(x)的图象上.
中第一行第二列元素的余子式记为f(x),且关于x的不等式f(x)<0的解集为(-2,0).各项均为正数的数列{an}的前n项和为Sn,点列(an,Sn)(n∈N*)在函数y=f(x)的图象上.
(1)求函数y=f(x)的解析式;
(2)若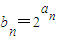 ,求
,求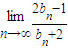 的值;
的值;
(3)令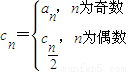 ,求数列{cn}的前20项之和.
,求数列{cn}的前20项之和.
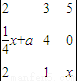 中第一行第二列元素的余子式记为f(x),且关于x的不等式f(x)<0的解集为(-2,0).各项均为正数的数列{an}的前n项和为Sn,点列(an,Sn)(n∈N*)在函数y=f(x)的图象上.
中第一行第二列元素的余子式记为f(x),且关于x的不等式f(x)<0的解集为(-2,0).各项均为正数的数列{an}的前n项和为Sn,点列(an,Sn)(n∈N*)在函数y=f(x)的图象上.(1)求函数y=f(x)的解析式;
(2)若
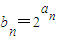 ,求
,求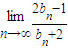 的值;
的值;(3)令
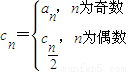 ,求数列{cn}的前20项之和.
,求数列{cn}的前20项之和.▼优质解答
答案和解析
【答案】分析:(1)由条件可知,f(x)=x2+ax,利用不等式f(x)<0的解集为(-2,0),可求a,从而可得函数y=f(x)的解析式;(2)利用点列(an,Sn)(n∈N*)在函数y=f(x)的图象上,可得所以Sn=+,利用当n≥...
看了 设a∈R,把三阶行列式中第一...的网友还看了以下:
f(x)=1-2/(log2x+1),咋算的设X1=a,X2=b其中a、b均大于2设f(x)=(l 2020-04-27 …
木板B放在粗糙的水平地面上,木块A放在B的上面,A的右端通过不可伸长的轻绳固定在竖直墙壁上用水平力 2020-06-03 …
已知函数f:[a,b]→R(实数集合),且对于任意x,y∈[a,b],f[(x+y)/2]≤[f( 2020-08-01 …
若函数f(x)不等于0,且f(x)满足下列三个条件:1.对任意实数a、b,均有f(a-b)=f(a 2020-08-03 …
EXCEL循环或计算问题。F=A+B+C+D+E。(A.B.C.D.E.F.均要大于零)E=A*10 2020-11-01 …
儿子的两道习题及解答理解不了,不知道什么涵义,求详解1.若对于一切实数a,b均有f(ab)=f(a) 2020-11-21 …
高一数学题1.若非0函数f(x)对任意实数A,B均有(a+b)=f(a)乘f(b),且当X小于零时, 2020-12-07 …
若非零函数f(x)对任意实数a,b均有f(a+b)=f(a)乘f(b),且当x大于零时,f(x)大于 2020-12-07 …
若非零函数f(x)对任意实数a,b均有f(a+b)=f(a)乘f(b),且当x大于零时,f(x)大于 2020-12-07 …
若非零函数F(x)对任意实数a,b均有f(a+b)=f(a)*f(b),且当x1:(1)求证:f(x 2020-12-07 …