早教吧作业答案频道 -->数学-->
如图,正方形ABCD,AM⊥MN,DN交BC延长线于F.(1)如图1,M为BC中点,AM=MN,则△CDF的形状是;(2)如图2,E是AB上一动点,M为EC中点,CF=CD,则AM与MN有怎样的数量关系?并证明你的结论.
题目详情
如图,正方形ABCD,AM⊥MN,DN交BC延长线于F.
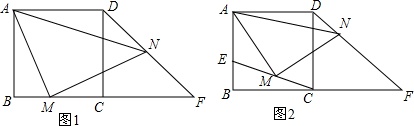
(1)如图1,M为BC中点,AM=MN,则△CDF的形状是___;
(2)如图2,E是AB上一动点,M为EC中点,CF=CD,则AM与MN有怎样的数量关系?并证明你的结论.
(1)如图1,M为BC中点,AM=MN,则△CDF的形状是___;
(2)如图2,E是AB上一动点,M为EC中点,CF=CD,则AM与MN有怎样的数量关系?并证明你的结论.

▼优质解答
答案和解析
(1)△CDF是等腰直角三角形;理由如下:
作NG⊥CF于G,如图1所示: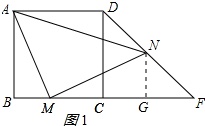
则∠MGN=90°,NG∥CD,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠B=∠BCD=90°,
∴∠DCF=90°,∠BAM+∠AMB=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMG=90°,
∴∠BAM=∠GMN,
在△ABM和△MGN中,
,
∴△ABM≌△MGN(AAS),
∴BM=GN,AB=MG,
∵M是BC的中点,
∴BM=CM=
BC,
∴GN=
BC=
CD,CG=CM,
∴GN是△CDF的中位线,
∴G是CF的中点,
∴CD=CF,
∴△CDF是等腰直角三角形;
故答案为:等腰直角三角形.
(2)AM=MN;理由如下:
连接BM、DM;如图2所示: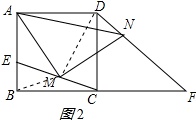
∵M为EC中点,∠B=90°,
∴MB=
EC=MC=EM,
∴∠MBC=∠MCB,
∴∠ABM=∠DCM,
在△ABM和△DCM中,
,
∴△ABM≌△DCM(SAS),
∴AM=DM,
∴∠MAD=∠ADM,
设∠MAD=∠ADM=x,
∴∠MDC=90°-x,
∴∠DMN=90°-(180°-2x)=2x-90°,
∵CF=CD,
∴∠F=∠CDF=45°,
∴∠MDN=135°-x,
∴∠DNM=180°-∠MDN-∠DMN=180°-(90°-x+45°)-(2x-90°)=135°-x,
∴∠MDN=∠MND,
∴MN=MD,
∴AM=MN.
作NG⊥CF于G,如图1所示:

则∠MGN=90°,NG∥CD,
∵四边形ABCD是正方形,
∴AB=BC=CD,∠B=∠BCD=90°,
∴∠DCF=90°,∠BAM+∠AMB=90°,
∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMG=90°,
∴∠BAM=∠GMN,
在△ABM和△MGN中,
|
∴△ABM≌△MGN(AAS),
∴BM=GN,AB=MG,
∵M是BC的中点,
∴BM=CM=
| 1 |
| 2 |
∴GN=
| 1 |
| 2 |
| 1 |
| 2 |
∴GN是△CDF的中位线,
∴G是CF的中点,
∴CD=CF,
∴△CDF是等腰直角三角形;
故答案为:等腰直角三角形.
(2)AM=MN;理由如下:
连接BM、DM;如图2所示:

∵M为EC中点,∠B=90°,
∴MB=
| 1 |
| 2 |
∴∠MBC=∠MCB,
∴∠ABM=∠DCM,
在△ABM和△DCM中,
|
∴△ABM≌△DCM(SAS),
∴AM=DM,
∴∠MAD=∠ADM,
设∠MAD=∠ADM=x,
∴∠MDC=90°-x,
∴∠DMN=90°-(180°-2x)=2x-90°,
∵CF=CD,
∴∠F=∠CDF=45°,
∴∠MDN=135°-x,
∴∠DNM=180°-∠MDN-∠DMN=180°-(90°-x+45°)-(2x-90°)=135°-x,
∴∠MDN=∠MND,
∴MN=MD,
∴AM=MN.
看了如图,正方形ABCD,AM⊥M...的网友还看了以下:
朱自清《春》春草图的评析最好长点明早就要快 2020-04-07 …
直角三角形斜边上有三个正方形,边长分别为a、b、c,求a、b、c的关系直角三角形斜边上有三个正方形 2020-05-20 …
童年摘抄好句好段10页!最好长点!明天报名! 2020-06-13 …
如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、 2020-07-22 …
A、B是圆的直径的两个端点,亮亮在A点,明明在B点,他们同时出发,反向而行,他们在C点第一次相遇, 2020-07-30 …
动手操作:小明利用等距平行线解决了二等分线段的问题.作法:(1)在e上任取一点C,以点C为圆心,A 2020-08-02 …
已知∠MON=90°,点A,B分别在射线ON,OM上运动,∠OAB的平分线与三角形OBA的外角∠A 2020-08-03 …
下列旅游景点中属于北京市的有()A.长城、故宫、天坛、颐和园、圆明园B.长城、承德避暑山庄、故宫、天 2020-11-12 …
用圆规求做一点P使点p点a所所在直线与L平行(2)画法:在直线l上任取B,C两点,以点A为圆心,BC 2020-12-01 …
探究:在图中找出一组相等的线段(半径除外),并证明你的结论.OA,OB是圆O的半径,且OA垂直OB, 2020-12-05 …