早教吧作业答案频道 -->数学-->
如图所示,在平面直角坐标系中,线段AB的端点A在y轴上,端点B在x轴上,BF平分∠ABO并与△ABO的外角平分线AE所在的直线交于点F.(1)求∠F的大小;(2)当点A、点B分别在y轴的正半轴和x轴
题目详情
如图所示,在平面直角坐标系中,线段AB的端点A在y轴上,端点B在x轴上,BF平分∠ABO并与△ABO的外角平分线AE所在的直线交于点F.
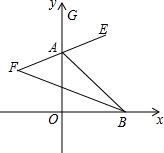
(1)求∠F的大小;
(2)当点A、点B分别在y轴的正半轴和x轴的正半轴上移动时,其它条件不变,(1)中结论还成立吗?说说你的理由.

(1)求∠F的大小;
(2)当点A、点B分别在y轴的正半轴和x轴的正半轴上移动时,其它条件不变,(1)中结论还成立吗?说说你的理由.
▼优质解答
答案和解析
(1)∵BF平分∠ABO,∠AE平分∠BAG,
∴∠ABF=
∠ABO,∠BAE=
∠BAG,
∵∠BAG=∠ABO+∠AOB,
∴∠BAE=
(∠ABO+∠AOB)=∠F+∠ABF,
∴∠F=
∠AOB=45°.
(2)(1)中结论成立,理由如下:
∵BF平分∠ABO,∠AE平分∠BAG,
∴∠ABF=
∠ABO,∠BAE=
∠BAG,
∵∠BAG=∠ABO+∠AOB,
∴∠BAE=
(∠ABO+∠AOB)=∠F+∠ABF,
∴∠F=
∠AOB=45°.
∴∠ABF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BAG=∠ABO+∠AOB,
∴∠BAE=
| 1 |
| 2 |
∴∠F=
| 1 |
| 2 |
(2)(1)中结论成立,理由如下:
∵BF平分∠ABO,∠AE平分∠BAG,
∴∠ABF=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BAG=∠ABO+∠AOB,
∴∠BAE=
| 1 |
| 2 |
∴∠F=
| 1 |
| 2 |
看了 如图所示,在平面直角坐标系中...的网友还看了以下:
导数f(x)=e^x+sinx,g(x)=ax.F(x)=f(x)-g(x).(1)x=0是F(x) 2020-03-30 …
数学上一般用f(x)来表示关于x的函数,若存在x∈R,使f(x)=x则称x为f(x)的不动点.已知 2020-05-13 …
f(x)=x^3+ax^2-a^2x+m(a>0)若对任意的a∈[3,6],不等式f(x)≤1在X 2020-05-16 …
已知x=1为函数f(x)=(x^2-ax+1)e^x的一个极值点,求a及函数f(x)的单调区间?急 2020-06-27 …
定义gx=fx-x的零点x0为不动点已知函数fx=ax2+(b+1)x+b-1(a≠0)问题在补充 2020-07-30 …
对于函数f(x),存在x∈R,使f(x)=x成立,则x称为f(X)的不动点已知函数f(x)=ax^ 2020-07-30 …
关于函数不动点对于函数f(x)=(2x+a)/(x+b)有合适f(x)=x的x时,这个x叫做f(x) 2020-10-30 …
已知f(x)=e^x,g(x)=lnx(1)求证g(x)<x<f(x)(2)设直线L与f(x),g( 2020-10-31 …
已知函数f(x)=1/3*x^3+[(1-a)/2]*x^2-ax-a,x∈R其中a>0.若函数f( 2020-11-10 …
已知函数f(x)=ax^2-bx+1若f(x)>0的解集是(-3,4),求实数a,b的值;若a为整数 2020-12-31 …