公元263年左右，我国数学家刘徽发现，当圆内接正多边形的边数无限增加时，正多边形的周长可无限逼近圆的周长，并创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的

Question

公元263年左右，我国数学家刘徽发现，当圆内接正多边形的边数无限增加时，正多边形的周长可无限逼近圆的周长，并创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的徽率，利用刘徽的割圆术设计的程序框图如图所示，若输出的n=96，则判断框内可以填入（　　）（参考数据：sin7.5°≈0.1305，sin3.75°≈0.06540，sin1.875°≈0.03272）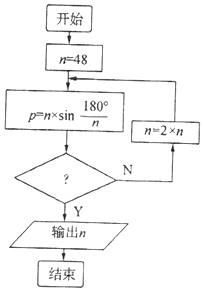

A. p≤3.14

B. p≥3.14

C. p≥3.1415

D. p≥3.1415926

Answer 1

模拟执行程序，可得：
n=48，p=48sin（(180)/(48)）°≈3.13，
n=96，S=96×sin（(180)/(96)）°≈3.14，
满足条件p≥3.14，退出循环，输出n的值为96．
故选：B．