公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形的面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位

Question

公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形的面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，其中n表示圆内接正多边形的边数，执行此算法输出的圆周率的近似值依次为（参考数据：

√(3)≈1.732，sin15°≈0.2588，sin75°≈0.1305）（　　）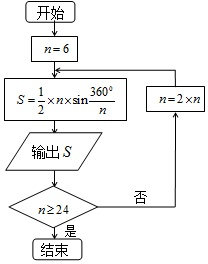

A. 2.598，3，3.1048

B. 2.598，3，3.1056

C. 2.578，3，3.1069

D. 2.588，3，3.1108

Answer 1

当n=6时，S=(1)/(2)×6×sin60°=2.598，输出S=2.598，
6<24，继续循环，当n=12时，S=(1)/(2)×12×sin30°=3，输出S=3，
12<24，继续循环，当n=24时，S=(1)/(2)×24×sin15°=3.1056，输出S=3.1056，
24=24，结束，
∴故选B．