公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似

Question

公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3，14，这就是著名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的n值为（　　）
参考数据：

√(3)=1.732，sin15°≈0.2588，sin7.5°≈0.1305．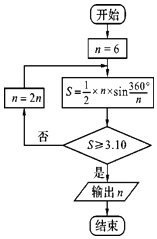

A. 12

B. 24

C. 48

D. 96

Answer 1

模拟执行程序，可得：
n=6，S=3sin60°=(3√(3))/(2)，
不满足条件S≥3.10，n=12，S=6×sin30°=3，
不满足条件S≥3.10，n=24，S=12×sin15°=12×0.2588=3.1056，
满足条件S≥3.10，退出循环，输出n的值为24．
故选：B．