早教吧作业答案频道 -->数学-->
如图,在四棱锥S-ABCD中,已知底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,tan∠SDA=23.(1)求四棱锥S-ABCD的体积;(2)在棱SD上找一点E,使CE∥平面SAB,并证明.
题目详情
如图,在四棱锥S-ABCD中,已知底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,SA=AB=BC=2,tan∠SDA=
.
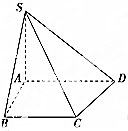
(1)求四棱锥S-ABCD的体积;
(2)在棱SD上找一点E,使CE∥平面SAB,并证明.
| 2 |
| 3 |

(1)求四棱锥S-ABCD的体积;
(2)在棱SD上找一点E,使CE∥平面SAB,并证明.
▼优质解答
答案和解析
(1)∵SA⊥底面ABCD,AD⊂平面ABCD,
∴SA⊥AD.
∵tan∠SDA=
=
,SA=2,∴AD=3.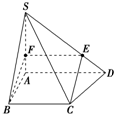
∴S梯形ABCD=
(BC+AD)×AB=5.
∴VS-ABCD=
S梯形ABCD×SA=
×5×2=
.
(2)当点E位于棱SD上靠近D的三等分点处时,可使CE∥平面SAB.
取SD上靠近D的三等分点为E,取SA上靠近点A的三等分点为F,连接CE,EF,BF,
则△SFE∽△SAB,∴
=
=
,
∴EF∥AD,EF=2,
又∵BC∥AD,BC=2,
∴BC∥EF,BC=EF.
∴四边形BCEF是平行四边形.
∴CE∥BF.又∵BF⊂平面SAB,CE⊄平面SAB,
∴CE∥平面SAB.
∴SA⊥AD.
∵tan∠SDA=
| SA |
| AD |
| 2 |
| 3 |

∴S梯形ABCD=
| 1 |
| 2 |
∴VS-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 10 |
| 3 |
(2)当点E位于棱SD上靠近D的三等分点处时,可使CE∥平面SAB.
取SD上靠近D的三等分点为E,取SA上靠近点A的三等分点为F,连接CE,EF,BF,
则△SFE∽△SAB,∴
| EF |
| AD |
| SF |
| SA |
| 2 |
| 3 |
∴EF∥AD,EF=2,
又∵BC∥AD,BC=2,
∴BC∥EF,BC=EF.
∴四边形BCEF是平行四边形.
∴CE∥BF.又∵BF⊂平面SAB,CE⊄平面SAB,
∴CE∥平面SAB.
看了如图,在四棱锥S-ABCD中,...的网友还看了以下:
(2013•贵阳二模)如图,在三棱柱ADF-BCE中,侧棱AB底面ADF,底面ADF是等腰直角三角 2020-04-08 …
\如图,四棱锥P-ABCD的底面为矩形,且AB=根号2,BC=1,E,F分别为AB,PC中点.(1 2020-05-16 …
如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2 2020-05-23 …
如图,在三棱锥D-ABC中,平面ADC垂直平面ABC,AD垂直平面DCB,AD=CD=2,AB=4 2020-06-15 …
在正方形ABCD-A‘B‘C‘D中棱长为a求三棱锥B‘-ABC的体积面AB‘C与面AB在正方形AB 2020-06-27 …
(2014•重庆模拟)在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面 2020-07-09 …
如图,在直三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB 2020-07-31 …
四棱锥A-DBCE中,O为地面正方形DBEC对角线的交点,F为AB的中点,求证AB//面DCF== 2020-07-31 …
(1)顶点在同一球面上的四棱柱ABCD-A1B1C1D1中,AB=1,AA1=庚号下2,则A,C两 2020-08-02 …
在四棱锥P-ABCD中,底面ABCD是矩形,DA⊥平面ABP,E是棱AB的中点,F在棱BC上,且AP 2020-11-04 …