早教吧作业答案频道 -->数学-->
在四棱锥P-ABCD中,底面ABCD是矩形,DA⊥平面ABP,E是棱AB的中点,F在棱BC上,且AP=BP=2,AB=2,AD=3,BF=2.(Ⅰ)求证:DF⊥平面EFP;(Ⅱ)求三棱锥E-DFP的体积.
题目详情
在四棱锥P-ABCD中,底面ABCD是矩形,DA⊥平面ABP,E是棱AB的中点,F在棱BC上,且AP=BP=
,AB=2,AD=3,BF=2.
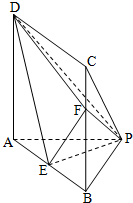
(Ⅰ)求证:DF⊥平面EFP;
(Ⅱ)求三棱锥E-DFP的体积.
| 2 |

(Ⅰ)求证:DF⊥平面EFP;
(Ⅱ)求三棱锥E-DFP的体积.
▼优质解答
答案和解析
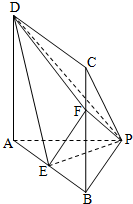 证明:(Ⅰ)因为AP=BP,E为AB的中点,所以PE⊥AB.
证明:(Ⅰ)因为AP=BP,E为AB的中点,所以PE⊥AB.
因为DA⊥平面ABP,PE⊂平面ABP,所以DA⊥PE,
又因为DA∩AB=A,DA⊂平面ABCD,AB⊂平面ABCD,
所以PE⊥平面ABCD,又DF⊂平面ABCD,
所以PE⊥DF.
在Rt△DCF中,DF=
=
;
在Rt△DAE中,DE=
=
;
在Rt△BEF中,EF=
=
.
所以DE2=DF2+EF2,因此DF⊥EF.
又因为PE⊥DF,PE⊂平面EFP,EF⊂平面EFP,EF∩PE=E,
所以DF⊥平面EFP.
(Ⅱ)由(Ⅰ)知PE⊥平面ABCD,故PE为三棱锥P-DEF的高,
在△ABP中,AP=BP=
,AB=2,所以AB2=AP2+BP2,得AP⊥BP,
又E是AB的中点,所以PE=
AB=1.
由(Ⅰ)得DF⊥EF,故S△DEF=
×DF×EF=
,
所以VE-DFP=VP-DEF=
×
×1=
.
 证明:(Ⅰ)因为AP=BP,E为AB的中点,所以PE⊥AB.
证明:(Ⅰ)因为AP=BP,E为AB的中点,所以PE⊥AB.因为DA⊥平面ABP,PE⊂平面ABP,所以DA⊥PE,
又因为DA∩AB=A,DA⊂平面ABCD,AB⊂平面ABCD,
所以PE⊥平面ABCD,又DF⊂平面ABCD,
所以PE⊥DF.
在Rt△DCF中,DF=
| DC2+CF2 |
| 5 |
在Rt△DAE中,DE=
| DA2+AE2 |
| 10 |
在Rt△BEF中,EF=
| BE2+BF2 |
| 5 |
所以DE2=DF2+EF2,因此DF⊥EF.
又因为PE⊥DF,PE⊂平面EFP,EF⊂平面EFP,EF∩PE=E,
所以DF⊥平面EFP.
(Ⅱ)由(Ⅰ)知PE⊥平面ABCD,故PE为三棱锥P-DEF的高,
在△ABP中,AP=BP=
| 2 |
又E是AB的中点,所以PE=
| 1 |
| 2 |
由(Ⅰ)得DF⊥EF,故S△DEF=
| 1 |
| 2 |
| 5 |
| 2 |
所以VE-DFP=VP-DEF=
| 1 |
| 3 |
| 5 |
| 2 |
| 5 |
| 6 |
看了在四棱锥P-ABCD中,底面A...的网友还看了以下:
真命题,底面是正多边形的直棱柱叫正棱柱下列命题是真命题的是A.有两个面平行,其余各面都是四边形的几 2020-04-27 …
给出下列命题中正确的是()A.棱柱被平面分成的两部分可以都是棱柱B.底面是矩形的平行六面体是长方体 2020-05-13 …
如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为π3,且侧面ABB1A 2020-05-17 …
1.正棱锥的对角面均垂直底面错在哪里?2.下面不是正棱锥的是A底面是正多边形,侧棱与底面所成的角都 2020-06-27 …
下列命题正确的是A一个侧面是矩形的棱柱是侧棱柱B两个侧面是矩形的棱柱是直棱柱C两个相邻侧面垂直于底 2020-07-04 …
下列命题中正确的是()A有两个面互相平行,其余各面都是四边形的几何体叫棱柱B棱柱中互相平行的两个面 2020-07-05 …
下列命题中正确的是()A.侧棱都相等的棱锥是正棱锥B.侧面与底面所成的角都相等的棱锥是正棱锥C.底 2020-07-30 …
1.已知三棱锥A-BCD中,AB=CD=根号5,BC=AD=根号13,BD=AC=根号10,则三棱 2020-07-30 …
一个棱锥的每条侧棱在底面的射影都相等,每个侧面与底面所成的角也都相等,那么[]A.它不是正棱锥B. 2020-07-30 …
下列说法错误的是()A.用平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台 2020-07-31 …