过山车是游乐场中常见的设施．如图是一种过山车运动轨道的简易模型，它由竖直平面内粗糙斜面轨道和光滑圆形轨道组成．过山车和斜面轨道间的动摩擦因数为μ，圆形轨道半径为R，A点是

Question

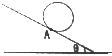
过山车是游乐场中常见的设施．如图是一种过山车运动轨道的简易模型，它由竖直平面内粗糙斜面轨道和光滑圆形轨道组成．过山车和斜面轨道间的动摩擦因数为μ，圆形轨道半径为R，A点是圆形轨道与斜面轨道的切点．过山车（可视为质点）从倾角为θ的斜面轨道某一点由静止开始释放并顺利通过圆形轨道．若整个过程中，人能承受过山车对他的作用力不超过其自身重力的8倍．求过山车释放点距A点的距离范围．

Answer 1

当人刚好到达圆轨道最高点时，由重力充当向心力，由牛顿第二定律得：
mg=m(v20)/(R)
由动能定理得：mg[s₀sinθ-R（1+cosθ）]-μmgs₀cosθ=(1)/(2)m

v

2 0

联立解得：s₀=(R(3+2cosθ))/(2(sinθ-μcosθ))
人在圆轨道时对轨道的最低点压力最大，由牛顿第三定律得：轨道对人最大支持力为8mg
由牛顿第二定律得：8mg-mg=m(v2)/(R)
由动能定理得：mg[s₁sinθ+R（1-cosθ）]-μmgs₁cosθ=(1)/(2)mv2
联立解得 s₁=(R(5+2cosθ))/(2(sinθ-μcosθ))
故过山车释放点距A点的距离范围为 (R(3+2cosθ))/(2(sinθ-μcosθ))≤s≤(R(5+2cosθ))/(2(sinθ-μcosθ))．
答：过山车释放点距A点的距离范围为 (R(3+2cosθ))/(2(sinθ-μcosθ))≤s≤(R(5+2cosθ))/(2(sinθ-μcosθ))．