如图，已知两点A（4，0），B（0，4），从点P（2，0）射出的光线经直线AB反射后射到直线OB上，再经直线OB反射后射到P点，则光线所经过的路程PM+MN+NP等于（）A.210B.6C.33D.25

Question

如图，已知两点A（4，0），B（0，4），从点P（2，0）射出的光线经直线AB反射后射到直线OB上，再经直线OB反射后射到P点，则光线所经过的路程PM+MN+NP等于（　　）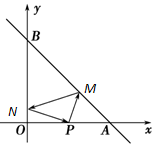

A. 2

√(10)

B. 6

C. 3

√(3)

D. 2

√(5)

Answer 1

由题意知y=-x+4的点A（4，0），点B（0，4）则点P（2，0）
设光线分别射在AB、OB上的M、N处，由于光线从点P经两次反射后又回到P点，
根据反射规律，则∠PMA=∠BMN；∠PNO=∠BNM．
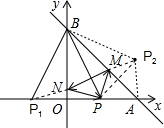
作出点P关于OB的对称点P₁，作出点P关于AB的对称点P₂，则：
∠P₂MA=∠PMA=∠BMN，∠P₁NO=∠PNO=∠BNM，
∴P₁，N，M，P₂共线，
∵∠P₂AB=∠PAB=45°，
即P₂A⊥OA；
PM+MN+NP=P₂M+MN+P₁N=P₁P₂═2√(10)；
，
故选：A．