早教吧作业答案频道 -->数学-->
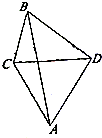
如图,某炮兵阵地位于A点,两观察所分别位于C、D两点,已知△ACD为正三角形,且DC=3km,当目标出现在B时,测得∠CDB=45°,∠BCD=75°,求炮兵阵地与目标的距离是多少?(精确到0.01km)
题目详情
如图,某炮兵阵地位于A点,两观察所分别位于C、D两点,已知△ACD为正三角形,且DC=
km,当目标出现在B时,测得∠CDB=45°,∠BCD=75°,求炮兵阵地与目标的距离是多少?(精确到0.01km)
| 3 |

▼优质解答
答案和解析
∵∠CDB=45°,∠BCD=75°,∴∠CBD=60°.
在△BCD中,由正弦定理得
=
,即
=
,
解得BC=
.
∵△ACD为正三角形,∴AC=
,∠ACD=60°,∴∠ACB=135°.
在△ABC中,由余弦定理得:AB2=BC2+AC2-2BC•AC•cos∠ACB=2+3-2
=5+2
.
∴AB=
≈2.91(km).
在△BCD中,由正弦定理得
| CD |
| sin∠CBD |
| BC |
| sin∠BDC |
| ||
| sin60° |
| BC |
| sin45° |
解得BC=
| 2 |
∵△ACD为正三角形,∴AC=
| 3 |
在△ABC中,由余弦定理得:AB2=BC2+AC2-2BC•AC•cos∠ACB=2+3-2
| 3 |
| 3 |
∴AB=
5+2
|
看了如图,某炮兵阵地位于A点,两观...的网友还看了以下:
初二直角三角形与直角坐标系问题如下图,段A的坐标为(0,0),点C的坐标为(0,4),点B的坐标为 2020-04-26 …
一定质量的理想气体经历如图所示的状态变化,变化顺序由a→b→c→d,图中坐标轴上的符号p指气体压强 2020-05-13 …
已知数轴上A、B两点坐标分别为-3、-6,若在数轴找一点C,使得A与C的距离为4.找一点D,使得B 2020-05-16 …
在直角坐标平面上有点A,B,C,D四点,其中A(2,0),B(3,4),C(6,5),如果四边形A 2020-05-17 …
正方形ABCD相对顶点B,D坐标分别为(0,-1),(2,5),则A,C坐标分别为不要用斜率解 2020-05-17 …
现有A,B,C,D四种物质,已知A,B为黑色粉末,C,D为无色气体,A,B在高温下作用能生成D,A 2020-05-17 …
数轴上标出若干个点,每相邻两点相距一个长度单位,点A,B,C,D对应的数分别是数a,b,c,d,且 2020-06-27 …
现有A、B、C、D四种元素,前三种元素的离子结构都和氖原子具有相同的核外电子排布.A没有正价态的化 2020-07-29 …
在平面直角坐标系中,点A(0,2),B(0,-2),C(8,-2),D(8,2).顺次连接A,B, 2020-07-30 …
如图a,在平面直角坐标系中,点A,B的坐标分别为(1,0),(-3,0),现同时将点A,B分别向上平 2020-12-14 …