早教吧作业答案频道 -->数学-->
课题学习:平行线的“等角转化”功能阅读理解如图1,已知点A是BC外一点,连接AB、AC,求∠BAC+∠B∠C的度数.(1)阅读并补充下面推理过程.过点A作DE∥BC,所以∠B=,∠C=.又∵
题目详情
课题学习:平行线的“等角转化”功能
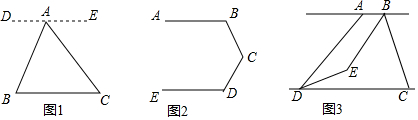
【阅读理解】如图1,已知点A是BC外一点,连接AB、AC,求∠BAC+∠B∠C的度数.
(1)阅读并补充下面推理过程.
过点A作DE∥BC,所以∠B=___,∠C=___.
又∵∠DAB+∠BAC+∠EAC=180°
∴∠B+∠BAC+∠C=180°
【解题反思】从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
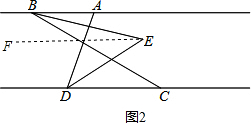
【方法运用】(2)如图2,已知AB∥CD,点C在点D的右侧,∠ADC=50°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间,如图3,若∠ABC=n°,求∠BED的度数(用含n的代数式表示)
【阅读理解】如图1,已知点A是BC外一点,连接AB、AC,求∠BAC+∠B∠C的度数.
(1)阅读并补充下面推理过程.
过点A作DE∥BC,所以∠B=___,∠C=___.
又∵∠DAB+∠BAC+∠EAC=180°
∴∠B+∠BAC+∠C=180°
【解题反思】从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
【方法运用】(2)如图2,已知AB∥CD,点C在点D的右侧,∠ADC=50°,BE平分∠ABC,DE平分∠ADC,BE,DE所在的直线交于点E,点E在AB与CD两条平行线之间,如图3,若∠ABC=n°,求∠BED的度数(用含n的代数式表示)

▼优质解答
答案和解析
 【阅读理解】(1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,
【阅读理解】(1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,
故答案为:∠EAD,∠DAE;
【解题反思】过C作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠D=∠FCD,
∵CF∥AB,
∴∠B=∠BCF,
∵∠BCF+∠BCD+∠DCF=360°,
∴∠B+∠BCD+∠D=360°,
【方法运用】(2)A、如图2,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=70°,
∴∠ABE=
∠ABC=30°,∠CDE=
∠ADC=35°,
∴∠BED=∠BEF+∠DEF=30°+35°=65°;
故答案为:65;
B、如图3,过点E作EF∥AB,
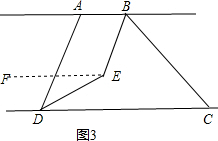 ∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∴∠ABE=
∠ABC=
n°,∠CDE=
∠ADC=35°
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°-∠ABE=180°-
n°,∠CDE=∠DEF=35°,
∴∠BED=∠BEF+∠DEF=180°-
n°+35°=215°-
n°.
 【阅读理解】(1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,
【阅读理解】(1)∵ED∥BC,∴∠B=∠EAD,∠C=∠DAE,故答案为:∠EAD,∠DAE;
【解题反思】过C作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠D=∠FCD,
∵CF∥AB,
∴∠B=∠BCF,
∵∠BCF+∠BCD+∠DCF=360°,
∴∠B+∠BCD+∠D=360°,
【方法运用】(2)A、如图2,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=70°,
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BED=∠BEF+∠DEF=30°+35°=65°;
故答案为:65;
B、如图3,过点E作EF∥AB,
 ∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=70°∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°-∠ABE=180°-
| 1 |
| 2 |
∴∠BED=∠BEF+∠DEF=180°-
| 1 |
| 2 |
| 1 |
| 2 |
看了课题学习:平行线的“等角转化”...的网友还看了以下:
1.一个角一定是平面图形吗?2.二面角到底是不是角呢?如果是角,它是平面角么?3.如果角不一定是平 2020-06-04 …
关于二面角的问题如何两个平面重合,那么他们所成的二面角是180度还是0度?那如果两个平面平行,那么 2020-06-27 …
您好,在用向量法求二面角时怎样快速判断二面角的平面角是锐角还是钝角呢? 2020-06-27 …
下列说法:①两个相交平面组成的图形叫做二面角;②两条异面直线分别和一个二面角的两个半平面垂直,则这 2020-06-27 …
下列命题正确的个数为()①斜线与它在平面内的射影所成的角是这条斜线和这个平面内所有直线所成的角的最 2020-07-30 …
怎么判断二面角是钝角还是锐角用肉眼观察时,经常看不懂(女生空间想象能力较差),有什么技巧吗?另,老 2020-07-30 …
关于两平面夹角的问题两平面的夹角就是二面角吗?取值范围是多少?有人说两平面的夹角是两个角,二面角是 2020-07-31 …
求平面角问题.直角三角形ABC中,角ABC=90度,角BAC=45度,PA垂直于平面ABC,且PA 2020-07-31 …
空间向量法如何判断二面角是钝角还是锐角请哥哥姐姐们细细看我要问的问题有人说从图上直接可以看出二面角 2020-08-02 …
有以下4个命题:①斜线与它在平面内的射影所成的角是这条斜线和这个平面内所有直线所成的角的最小角;②二 2020-12-05 …