早教吧作业答案频道 -->数学-->
已知点A在数轴上对应的数为a,点B对应的数为b,且|a+2|+(b-5)2=0,规定A、B两点之间的距离记作AB=|a-b|(1)求A、B两点之间的距离AB;(2)设点P在线段AB之间且在数轴上对应的数为x,当PA+PB=1
题目详情
已知点A在数轴上对应的数为a,点B对应的数为b,且|a+2|+(b-5)2=0,规定A、B两点之间的距离记作AB=|a-b|
(1)求A、B两点之间的距离AB;
(2)设点P在线段AB之间且在数轴上对应的数为x,当PA+PB=10时,求x的值;
(3)若点P在线段AB之外,N、M分别是PA、PB的中点.对于(1)PN+PM的值,(2)|PN-PM|的值.探究(1)(2)中值的结果,判断哪个结果的值一定是一个常数,说明理由并求出这个常数.
(1)求A、B两点之间的距离AB;
(2)设点P在线段AB之间且在数轴上对应的数为x,当PA+PB=10时,求x的值;
(3)若点P在线段AB之外,N、M分别是PA、PB的中点.对于(1)PN+PM的值,(2)|PN-PM|的值.探究(1)(2)中值的结果,判断哪个结果的值一定是一个常数,说明理由并求出这个常数.
▼优质解答
答案和解析
 (1)∵|a+2|+(b-5)2=0,
(1)∵|a+2|+(b-5)2=0,
∴a=-2,b=5,
∴AB=|a-b|=|-2-5|=7;
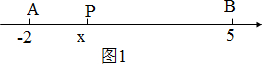
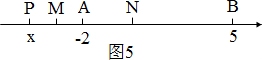
(2)如图1,若点P在A、B之间
PA=|x-(-2)|=x+2,
PB=|x-5|=5-x.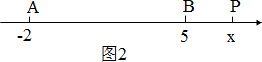
∴PA+PB=x+2+5-x=7<10
∴点P在A、B之间不合题意,舍去;
如图2,若点P在AB的延长线上时
PA=|x-(-2)|=x+2,
PB=|x-5|=x-5.
∵PA+PB=10,
∴x+2+x-5=10,
解,得x=
;
如图3,若点P在AB的反向延长线上时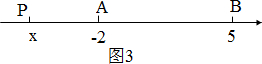
PA=|x-(-2)|=-2-x
PB=|x-5|=5-x.
∵PA+PB=10,
∴-2-x+5-x=10,
解,得x=-
.
综上所述,当PA+PB=10时,x值为
,-
.
(3)(2)的值是一个常数,理由如下:
当点P在线段AB的右侧时,如图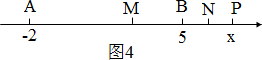
有PN-PM=
PB-
PA=
(PB-PA)=
AB=-
当点P线段AB的左侧时,如图
有PN-PM=
PB-
PA=
(PB-PA)=
AB=
.
∴点P在线段AB之外时,总有|PN-PM|=
 (1)∵|a+2|+(b-5)2=0,
(1)∵|a+2|+(b-5)2=0,∴a=-2,b=5,
∴AB=|a-b|=|-2-5|=7;
(2)如图1,若点P在A、B之间
PA=|x-(-2)|=x+2,
PB=|x-5|=5-x.

∴PA+PB=x+2+5-x=7<10
∴点P在A、B之间不合题意,舍去;
如图2,若点P在AB的延长线上时
PA=|x-(-2)|=x+2,
PB=|x-5|=x-5.
∵PA+PB=10,
∴x+2+x-5=10,
解,得x=
| 13 |
| 2 |
如图3,若点P在AB的反向延长线上时

PA=|x-(-2)|=-2-x
PB=|x-5|=5-x.
∵PA+PB=10,
∴-2-x+5-x=10,
解,得x=-
| 7 |
| 2 |
综上所述,当PA+PB=10时,x值为
| 13 |
| 2 |
| 7 |
| 2 |
(3)(2)的值是一个常数,理由如下:
当点P在线段AB的右侧时,如图

有PN-PM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
当点P线段AB的左侧时,如图
有PN-PM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
∴点P在线段AB之外时,总有|PN-PM|=
| 7 |
| 2 |

看了已知点A在数轴上对应的数为a,...的网友还看了以下:
根据下列条件,写出二次函数的解析式1.当x=2时,函数的最大值是1,且图像与x轴的两个交点之间的距离 2020-03-30 …
(关于高中圆与直线的问题1.设点B是点A(2,-3,5)关于xOy平面的对称点,则A.B两点的距离 2020-04-27 …
求,带相聚和离别的对联.有无横批不重要最好,带有茶字 2020-05-12 …
硫元素位于元素周期表第列;硫元素原子核外有2个未成对电子,这2个电子所处亚层的符号是;硫、氯元素的 2020-05-14 …
椭圆x2/a2椭圆x^2/a^2+y^2/b^2=1(a>b>0)的左右焦点分别为F1、F2,过F 2020-05-15 …
(2012•锦州)如图,抛物线y=ax2+bx-3交y轴于点C,直线l为抛物线的对称轴,点P在第三 2020-06-11 …
大学物理,急求啊,不会的不要乱来,怒.一小珠可在半径为R的圆环上无摩擦的滑动,圆环绕其竖直直径的轴 2020-06-14 …
(2013•温州一模)某溶液X仅含下表离子中的5种(不考虑水的电离与离子水解),且各种离子的物质的 2020-06-16 …
设椭圆C:x2╱a2+y2╱b2=1(a>b>0)的离心率e为根号2╱2,点A是椭圆上的一点,且A 2020-06-30 …
快开学了,1)将平行四边形ABCD的对角线交点与直角坐标系的原点重合,且点A,B的坐标分别为(-2 2020-07-04 …