早教吧作业答案频道 -->数学-->
已知△ABC,D、E是射线BC上的两点,且BD=AB,CE=AC.(1)若AB=AC,且∠BAC=90°(如图),求证:AE2=BE•DE;(2)若△ABC是直角三角形,且AE2=BE•DE,求∠ABC的度数.(如果需要,自己画出符合条
题目详情
已知△ABC,D、E是射线BC上的两点,且BD=AB,CE=AC.
(1)若AB=AC,且∠BAC=90°(如图),求证:AE2=BE•DE;
(2)若△ABC是直角三角形,且AE2=BE•DE,求∠ABC的度数.(如果需要,自己画出符合条件的大致图形)
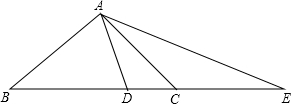
(1)若AB=AC,且∠BAC=90°(如图),求证:AE2=BE•DE;
(2)若△ABC是直角三角形,且AE2=BE•DE,求∠ABC的度数.(如果需要,自己画出符合条件的大致图形)

▼优质解答
答案和解析
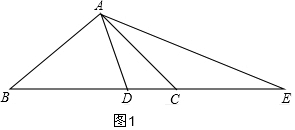 证明:(1)如图1,∵AB=AC,∠BAC=90°,
证明:(1)如图1,∵AB=AC,∠BAC=90°,
∴∠B=∠BCA=45°,
∠BAD=∠BDA=
=67.5°,
∴∠DAC=90°-67.5°=22.5°,
∵AC=CE,
∴∠E=∠CAE=22.5°,
∴∠EAD=45°,
∴∠EAD=∠B,
∵∠E=∠E,
∴△EAD∽△EBA,
∴
=
,
∴AE2=BE•DE;
(2)若△ABC是直角三角形,分三种情况讨论:
①当∠BAC=90°时,如图1,
∵AE2=BE•DE,
∴
=
,
∵∠E=∠E,
∴△ADE∽△BAE,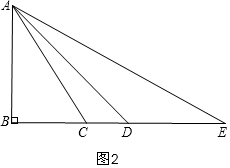
∴∠DAE=∠B,
设∠E=x°,
∵AC=CE,
∴∠CAE=∠E=x°,
∴∠ACB=2x°,
∵∠BAC=90°,
∴∠B=90°-2x°,
∵AB=AD,
∴∠BDA=∠BAD=
=45+x,
在△ADE中,∠DAE=∠B=90-2x,
∠ADB=∠DAE+∠E,
45+x=90-2x+x,
x=22.5°,
∴∠ABC=90-2x=45°;
②当∠ABC=90°时,如图2,
∵AE2=BE•DE,∠E=∠E,
∴△ADE∽△BAE,
但图2中,∠EAD≠∠B,
所以此种情况不成立;
③当∠ACB=90°时,如图3,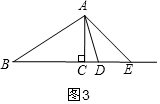
∵AC=CE,
∴∠CAE=∠E=45°,
∵AE2=BE•DE,∠E=∠E,
∴△ADE∽△BAE,
∴∠DAE=∠B,
设∠B=x°,则∠DAE=x°,∠BAC=90°-x°,
∴∠DAC=45°-x°,
∵AB=BD,
∴∠ADB=
=90°-
x°,
由∠BAD=∠ADB得:90-x+45-x=90-
x,
x=30°,
∴∠ABC=30°,
综上所述:∠ABC=45°或30°.
 证明:(1)如图1,∵AB=AC,∠BAC=90°,
证明:(1)如图1,∵AB=AC,∠BAC=90°,∴∠B=∠BCA=45°,
∠BAD=∠BDA=
| 180°-45° |
| 2 |
∴∠DAC=90°-67.5°=22.5°,
∵AC=CE,
∴∠E=∠CAE=22.5°,
∴∠EAD=45°,
∴∠EAD=∠B,
∵∠E=∠E,
∴△EAD∽△EBA,
∴
| AE |
| EB |
| ED |
| AE |
∴AE2=BE•DE;
(2)若△ABC是直角三角形,分三种情况讨论:
①当∠BAC=90°时,如图1,
∵AE2=BE•DE,
∴
| AE |
| BE |
| DE |
| AE |
∵∠E=∠E,
∴△ADE∽△BAE,

∴∠DAE=∠B,
设∠E=x°,
∵AC=CE,
∴∠CAE=∠E=x°,
∴∠ACB=2x°,
∵∠BAC=90°,
∴∠B=90°-2x°,
∵AB=AD,
∴∠BDA=∠BAD=
| 180-(90-2x) |
| 2 |
在△ADE中,∠DAE=∠B=90-2x,
∠ADB=∠DAE+∠E,
45+x=90-2x+x,
x=22.5°,
∴∠ABC=90-2x=45°;
②当∠ABC=90°时,如图2,
∵AE2=BE•DE,∠E=∠E,
∴△ADE∽△BAE,
但图2中,∠EAD≠∠B,
所以此种情况不成立;
③当∠ACB=90°时,如图3,

∵AC=CE,
∴∠CAE=∠E=45°,
∵AE2=BE•DE,∠E=∠E,
∴△ADE∽△BAE,
∴∠DAE=∠B,
设∠B=x°,则∠DAE=x°,∠BAC=90°-x°,
∴∠DAC=45°-x°,
∵AB=BD,
∴∠ADB=
| 180°-x° |
| 2 |
| 1 |
| 2 |
由∠BAD=∠ADB得:90-x+45-x=90-
| 1 |
| 2 |
x=30°,
∴∠ABC=30°,
综上所述:∠ABC=45°或30°.
看了已知△ABC,D、E是射线BC...的网友还看了以下:
关于x的一元二次方程ax²+bx+c=0(a≠0),给出以下说法①若Δ=b²-4ac>0,则方程c 2020-05-15 …
圆锥曲线若直线y=x-b与抛物线y2=2px(p>0)相交于不同两点A(x1,y1),B(x2,y 2020-06-12 …
同一直线上的AB两质点相距为s,它们向同一方向沿直线运动,A做速度为v的匀速直线运动,B从此时刻起 2020-06-12 …
若三角形ABC的面积为3根号3/2两边a,b的长是方程x的平方-3根号3x+6=0的两若三角形AB 2020-06-12 …
设θ为两个非零向量a,b的夹角,已知对任意实数t,|b+ta|的最小值为1.()A.若θ确定,则| 2020-07-21 …
一元二次方程ax平方+bx+c=0(a不等于0),若a与c异号,则方程A有两个不相等的实数根B有两 2020-08-01 …
初三一元两次公式法.若等腰三角形ABC的一边长A=10,另两边B,C恰好是方程++++若等腰三角形 2020-08-02 …
设a,b是两条不重合的直线,α,β是两个不同的平面,则下列命题中错误的是()A.若a⊥α,a⊥β,则 2020-11-02 …
命题:①若a+b+c=0,则b2-4ac≥0此题考查什么下列命题:①若a+b+c=0,则b2-4ac 2020-11-06 …
已知∠A=60°,若∠B的两边与∠A的两边互相垂直,则∠B=若∠B的两边与∠A的两边互相平行,则∠B 2020-12-01 …