十八世纪瑞士数学家欧拉证明了简单多面体的顶点数（V）、面树（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：（1）

Question

十八世纪瑞士数学家欧拉证明了简单多面体的顶点数（V）、面树（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单多面体模型，解答下列问题：

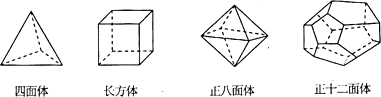
（1）根据上面多面体模型，填写表格中的空格：

多面体	顶点数（V）	面数（F）	棱数（E）
四面体	4	4	6
长方体	8	6	___
正八面体	___	8	12
正十二面体	20	12	30

（2）根据上面的表格，猜想顶点数（V）、面数（F）、棱数（E）之间存在的关系式是___（用所给的字母表达）；
（2）若一个多面体的面数比顶点数少14，且有48条棱，则这个多面体的面数是___；
（3）有一个玻璃饰品的外形是简单多面体，它共有24个顶点，每个顶点处都有3条棱，设该多面体的面数为x，求x的值．

Answer 1

（1）观察图形，长方体的棱数为12，正八面体的顶点数为6；
（2）观察表格可以看出：顶点数+面数-棱数=2，关系式为：V+F-E=2；
（3）由题意得：F+F+14-48=2，解得F=18；
（4）∵该多面体的顶点数V=24，且每个顶点处有3条棱，
∴该多面体的棱数E=(24×3)/(2)=36条，
设面数为x，
∵V+F-E=2，
∴24+x-36=2，
解得：x=14．
故答案为：（1）12，6；（2）V+F-E=2；（3）18．