设函数f（x）=2x，x≤0log2x，x>0，若对任意给定的m∈（1，+∞），都存在唯一的x∈R，满足f（f（x））=2a2m2+am，则正实数a的取值范围是（）A.[12，+∞)B.（12，+∞）C.[2，+∞）D.（2，+

Question

设函数f（x）=

2x，x≤0

log2x，x>0

，若对任意给定的m∈（1，+∞），都存在唯一的x∈R，满足f（f（x））=2a²m²+am，则正实数a的取值范围是（　　）

A. [

(1)/(2)，+∞)

B. （

(1)/(2)，+∞）

C. [2，+∞）

D. （2，+∞）

Answer 1

根据f（x）的函数，我们易得出其值域为：R，
又∵f（x）=2^x，（x≤0）时，值域为（0，1]；
f（x）=log₂x，（x>0）时，其值域为R，
∴可以看出f（x）的值域为（0，1]上有两个解，
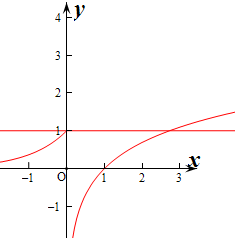
要想f（f（x））=ma+2m²a²，在a∈（1，+∞）上只有唯一的x∈R满足，
必有f（f（x））>1 （因为ma+2m²a²>0），
所以：f（x）>2，即log₂x>2，
解得：x>4，
当 x>4时，x与f（f（x））存在一一对应的关系，
∴ma+2m²a²>1，a∈（1，+∞），且m>0，
把m当作主变量，
则不等式等价为2m²a²+ma-1>0，
即（ma+1）（2ma-1）>0，
∵ma+1>0，
∴不等式等价为2ma-1>0，
即m>(1)/(2a)，
∵a>1，
∴(1)/(2a)<(1)/(2)，
则m≥(1)/(2)，
故正实数m的取值范围是[(1)/(2)，+∞）．
故选：A