早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,点A(10,0),B(4,8),C(0,8)点P从点O出发,沿O、A、B、C路线运动,到C点停止;点Q从C点出发,沿C、B、A、O路线运动,到O停止.若点P、Q同时出发,点P的
题目详情
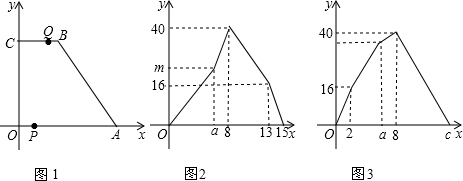
如图,在平面直角坐标系中,点A(10,0),B(4,8),C(0,8)点P从点O出发,沿O、A、B、C路线运动,到C点停止;点Q从C点出发,沿C、B、A、O路线运动,到O停止.若点P、Q同时出发,点P的速度为1cm/s,点Q的速度为2cm/s,a秒时四边形PABC为平行四边形,此时点P、Q同时改变速度,点P的速度变为bcm/s,点Q的速度为dcm/s.图2是点P出发x秒后△OPC的面积S1(cm2)与x(s)的函数关系图象,图3是点Q出发x秒后△OQC的面积S2(cm2)与x(s)的函数关系图象.
(1)参照图2、图3,求a、b、c及d、m的值.
(2)点Q运动几秒时,OQ⊥AB,并判断此时四边形OPQB的形状.
(3)设点P离开O的路程为y1(cm),点Q距O的路程为y2(cm),请分别写出点P、Q改变速度后,y1、y2与出发后的运动时间x(s)的函数关系式.并求出P、Q相遇时x的值.
(4)当x满足___条件时,点P、Q在运动路线上相距的路程不大于18cm.
(1)参照图2、图3,求a、b、c及d、m的值.
(2)点Q运动几秒时,OQ⊥AB,并判断此时四边形OPQB的形状.
(3)设点P离开O的路程为y1(cm),点Q距O的路程为y2(cm),请分别写出点P、Q改变速度后,y1、y2与出发后的运动时间x(s)的函数关系式.并求出P、Q相遇时x的值.
(4)当x满足___条件时,点P、Q在运动路线上相距的路程不大于18cm.

▼优质解答
答案和解析
(1)要使四边形PABC为平行四边形,需满足AP∥BC,且AP=BC,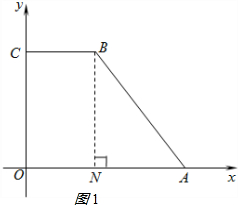
∵A(10,0),B(4,8),C(0,8),
∴BC=4cm,
∴OP=OA-AP=10-4=6cm,
∴a=6÷1=6s.
此时,S△OPC=
×6×8=24,m=24cm2,
8s时,S△OPC=
(6+2b)×8=40,
∴b=2cm/s.
如图1,过点B作BN⊥OA于点N,在△BMA中,BN=8cm,ON=BC=4cm,
∴AN=10-4=6cm,
∴AB=
=
=10cm,
当点P运动6s时,点Q运动到距离点A是2cm的位置,当时间为8s时,△OPC和△OQC的面积相等,即点P和点Q重合,
∴点Q改变速度后,2s运动的距离为2cm,
∴2d=2,d=1cm/s,
d(c-8)=10,c=18s.
(2)如图2,过点O作OM⊥AB于点M;连接PQ.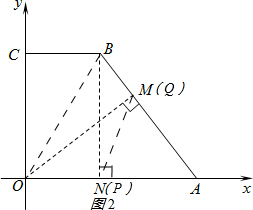
在△BNA和△OAM中,
,
∴△BNA≌△OAM(AAS),
∴AM=AN=6cm,
∴BM=AB-AM=10-6=4cm,
c当点Q运动到点M处时,OQ⊥AB,点Q运动的路程为:BC+BM=4+4=8cm,
∴点Q运动的时间为:8÷2=4s,
∴当Q运动4s时,OQ⊥AB.
当点Q运动4s时,点P运动4s,则点P运动到点N处,
在△AQP和△ABO中,
=
且∠QAP=∠BAO,
∴△AQP∽△ABO,
∴∠AQP=∠AB0,
∴QP∥BO.
又BQ=OP=4cm,
∴四边形OPQB为等腰梯形.
(3)由(1)可以,点P、Q运动6s后改变速度,
∴点P离开点O的路程为:y1=6+2(x-6)=2x-6;
点Q距离点O的距离为:y2=24-[12+(x-6)]=18-x,
点P、Q相遇时,y1=y2,即2x-6=18-x,解得:x=8s.
(4)根据题意,得|y2-y1|≤18,
即-18≤18-x-(2x-6)≤18,
解不等式组,得2≤x≤14.

∵A(10,0),B(4,8),C(0,8),
∴BC=4cm,
∴OP=OA-AP=10-4=6cm,
∴a=6÷1=6s.
此时,S△OPC=
| 1 |
| 2 |
8s时,S△OPC=
| 1 |
| 2 |
∴b=2cm/s.
如图1,过点B作BN⊥OA于点N,在△BMA中,BN=8cm,ON=BC=4cm,
∴AN=10-4=6cm,
∴AB=
| AN2+BN2 |
| 62+82 |
当点P运动6s时,点Q运动到距离点A是2cm的位置,当时间为8s时,△OPC和△OQC的面积相等,即点P和点Q重合,
∴点Q改变速度后,2s运动的距离为2cm,
∴2d=2,d=1cm/s,
d(c-8)=10,c=18s.
(2)如图2,过点O作OM⊥AB于点M;连接PQ.

在△BNA和△OAM中,
|
∴△BNA≌△OAM(AAS),
∴AM=AN=6cm,
∴BM=AB-AM=10-6=4cm,
c当点Q运动到点M处时,OQ⊥AB,点Q运动的路程为:BC+BM=4+4=8cm,
∴点Q运动的时间为:8÷2=4s,
∴当Q运动4s时,OQ⊥AB.
当点Q运动4s时,点P运动4s,则点P运动到点N处,
在△AQP和△ABO中,
| AQ |
| AB |
| AP |
| AO |
∴△AQP∽△ABO,
∴∠AQP=∠AB0,
∴QP∥BO.
又BQ=OP=4cm,
∴四边形OPQB为等腰梯形.
(3)由(1)可以,点P、Q运动6s后改变速度,
∴点P离开点O的路程为:y1=6+2(x-6)=2x-6;
点Q距离点O的距离为:y2=24-[12+(x-6)]=18-x,
点P、Q相遇时,y1=y2,即2x-6=18-x,解得:x=8s.
(4)根据题意,得|y2-y1|≤18,
即-18≤18-x-(2x-6)≤18,
解不等式组,得2≤x≤14.
看了 如图,在平面直角坐标系中,点...的网友还看了以下:
某景区的三个景点A,B,C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车 2020-04-06 …
如图已知直线y=4/3x+4与x轴,y轴分别交与A,B两点,点C从O点出发沿射线OA以每秒1个单位 2020-06-04 …
如图已知直线y=4/3x+4与x轴,y轴分别交与A,B两点,点C从O点出发沿射线OA以每秒1个单位 2020-06-04 …
几道函数题1已知点A(4,3),点B(0,1),若点C是x轴上一动点,当AC+BC的值最小时,求C 2020-07-30 …
在平面直角坐标系中,已知直线y=-3/4x+3与x轴,y轴分别交于A,B两点,点C(0,n)是y轴上 2020-11-03 …
驾驶证考试中的路考,在即将结束时要进行目标停车,考官会在离停车点不远的地方发出指令,要求将车停在指定 2020-11-14 …
往返于A,B两个城市的客车,中途有三个停靠点C,D,E,(1)该客车有多少种不同的票价?(2)该车要 2020-12-04 …
如图,线段AB上两点C、D,AB=30cm,AC=10cm,BD=5cm,点P从A出发以每秒1cm的 2020-12-15 …
某景区的三个景点A,B,C在同一线路上,甲,乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先 2020-12-27 …
直线y=-3/4x+3与x轴y轴分别交于A,B两点,点C(X,Y)是y=-3/4x+3的动点过点C的 2021-01-10 …