早教吧作业答案频道 -->数学-->
如图,已知直线AB的函数表达式为y=2x+10,与x轴交点为A,与y轴交点为B.(1)求A,B两点的坐标;(2)若点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF.是否存在点P,使
题目详情
如图,已知直线AB的函数表达式为y=2x+10,与x轴交点为A,与y轴交点为B.
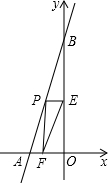
(1)求 A,B两点的坐标;
(2)若点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF.是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

(1)求 A,B两点的坐标;
(2)若点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF.是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
▼优质解答
答案和解析
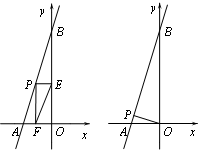
(1)∵一次函数y=2x+10,
令x=0,则y=10,令y=0,则x=-5,
∴点A坐标为(-5,0),点B坐标为(0,10);
(2)存在点P使得 EF 的值最小,
理由如下:
∵PE⊥y轴于点E,PF⊥x轴于点F,
∴四边形PEOF是矩形,且EF=OP,
∵O为定点,P在线段上AB运动,
∴当OP⊥AB时,OP取得最小值,此时EF最小,
∵点A坐标为(-5,0),点B坐标为(0,10),
∴OA=5,O B=10,
由勾股定理得:AB=5
∵∠AOB=90,OP⊥AB,
∴△AOB∽△OPB,
∴
=
,
∴OP=2
,
即存在点P使得 EF 的值最小,最小值为 2
.

(1)∵一次函数y=2x+10,
令x=0,则y=10,令y=0,则x=-5,
∴点A坐标为(-5,0),点B坐标为(0,10);
(2)存在点P使得 EF 的值最小,
理由如下:
∵PE⊥y轴于点E,PF⊥x轴于点F,
∴四边形PEOF是矩形,且EF=OP,
∵O为定点,P在线段上AB运动,
∴当OP⊥AB时,OP取得最小值,此时EF最小,
∵点A坐标为(-5,0),点B坐标为(0,10),
∴OA=5,O B=10,
由勾股定理得:AB=5
| 5 |
∵∠AOB=90,OP⊥AB,
∴△AOB∽△OPB,
∴
| AO |
| OP |
| AB |
| OB |
∴OP=2
| 5 |
即存在点P使得 EF 的值最小,最小值为 2
| 5 |
看了 如图,已知直线AB的函数表达...的网友还看了以下:
设函数f(x)在x=a的某个邻域内有定义,则f(x)在x=a处可导的一个充分条件是?请写出分析过程! 2020-03-30 …
已知函数f(x)对任意实数a,b有f(a)不等于0,f(a+b)=f(a)f(b),当x小于0时, 2020-05-19 …
f(a)的导数=x趋近于0,-[f(a-h)-f(a)]/h的极限吗?RT,哪里没懂我补充. 2020-05-20 …
已知a,b属于N*,f(a+b)=f(a)·f(b),f(1)=2则f(2)∕f(1)+f(3)∕ 2020-06-03 …
已知函数y=f(x)的定义域[-1,1],且f(-x)=-f(x),f(1)=1,当a,b属于[- 2020-06-27 …
设f(x),g(x)在[a,b]上连续,在(a,b)内可导,且g(x)不等于0,f(a)g(b)= 2020-07-21 …
f(x)在开区间(a,b)导数大于等于0,f(a)=0,为什么书上说f(x)在(a,b)上是大于0 2020-08-01 …
设f(x)在[a,b]上存在二阶导数,且f"(x)不等于0,f(a)=f(b)=0,试证在开区间( 2020-08-01 …
由牛顿第二定律可知,物体质量m=F/a,对于m,F,a三者的关系,下列说法正确的是Aa一定时,m跟F 2020-11-03 …
导数的定义的问题已知f'(a)=k,lim(x趋向于0)f(a+2x)-f(a-3x)/x的极限,答 2021-02-20 …