早教吧作业答案频道 -->数学-->
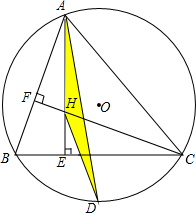
已知,△ABC内接于O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.
题目详情
已知,△ABC内接于 O,∠BAC=60°,AE⊥BC,CF⊥AB.AE,CF相交于点H,点D为弧BC的中点,连接HD,AD.求证:△AHD为等腰三角形.

▼优质解答
答案和解析
证明:连接AO、OD,过O作OM⊥AC,则AM=
AC,如图所示: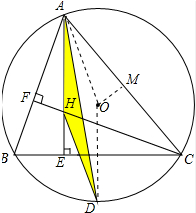
∵∠BAC=60°,CF⊥AB,
∴AF=
AC,
∴AM=AF,
∵AE⊥BC,CF⊥AB,
∴∠ABC+∠FHE=180°,
∵∠FHE+∠AHF=180°,
∴∠ABC=∠AHF,
∵∠AOM=
∠AOC=∠ABC,
∴∠AHF=∠AOM,
在△AMO与△AFH中,
,
∴△AMO≌△AFH(AAS),
∴AO=AH,
∵OD=OA,
∴AO=AH=OD,
∵点D为弧BC的中点,
∴OD⊥BC,
∵AE⊥BC,
∴AE∥OD,
∴四边形OAHD为平行四边形,
∵AO=AH,
∴四边形AHDO是菱形,
∴AH=HD,
∴△AHD为等腰三角形.
| 1 |
| 2 |

∵∠BAC=60°,CF⊥AB,
∴AF=
| 1 |
| 2 |
∴AM=AF,
∵AE⊥BC,CF⊥AB,
∴∠ABC+∠FHE=180°,
∵∠FHE+∠AHF=180°,
∴∠ABC=∠AHF,
∵∠AOM=
| 1 |
| 2 |
∴∠AHF=∠AOM,
在△AMO与△AFH中,
|
∴△AMO≌△AFH(AAS),
∴AO=AH,
∵OD=OA,
∴AO=AH=OD,
∵点D为弧BC的中点,
∴OD⊥BC,
∵AE⊥BC,
∴AE∥OD,
∴四边形OAHD为平行四边形,
∵AO=AH,
∴四边形AHDO是菱形,
∴AH=HD,
∴△AHD为等腰三角形.
看了已知,△ABC内接于O,∠BA...的网友还看了以下:
提示:D-C=0A-B,A-D,D-C,D-E,E-F=1A-D,C-F=2A-B,D-E,E-F 2020-04-06 …
在梯形ABCD中,AD平行BC,AB=AD=DC=2BC=4在等腰三角形PQR中,角QPR=120 2020-05-01 …
#includemain(){inta=0x7fffffff,b=025;floatf1=123. 2020-05-19 …
sprintf(sqls,"dasiinsert%d,'%s%d:%d',%d,%d",vid,b 2020-05-20 …
求光栅常数d一束具有两种波长a和d的平行光垂直照射到一衍射光栅上,测得波长a的第三极主极大衍射角和 2020-07-10 …
已知A,B,C,D和A+C,B+C,B+D,D+A分别表示1至8这八个自然数,且互不相等.如果A是 2020-07-22 …
对任意两个随机变量X和Y,由D(X+Y)=D(X)+D(Y)可以推断()X和Y不相关X和Y相互独立 2020-07-23 …
有一种无毒蛇的体表花纹颜色由D、d和H、h两对基因(独立遗传)控制,与性别无关.其花纹颜色与基因的对 2020-12-08 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
d(lny)/d(1/x).d(y)/d(lnx).这l两个个怎么求导还有lny=b1+b2(1/x 2021-02-03 …