早教吧作业答案频道 -->数学-->
如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,(1)求∠APB的度数.(2)求正方形ABCD的面积.
题目详情
如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,
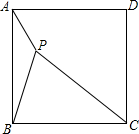
(1)求∠APB的度数.
(2)求正方形ABCD的面积.

(1)求∠APB的度数.
(2)求正方形ABCD的面积.
▼优质解答
答案和解析
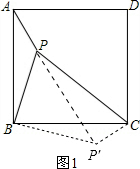 (1)如图1,将△ABP绕点B按顺时针方向旋转90°,使AB与BC重合;
(1)如图1,将△ABP绕点B按顺时针方向旋转90°,使AB与BC重合;
则∠PBP′=90°,BP′=BP=2,P′C=PA=1;
由勾股定理得:PP′2=22+22=8;
∵P′C2=12=1,PC2=32=9,
∴PC2=PP′2+P′C2,
∴∠PP′C=90°;而∠BP′P=45°,
∴∠BP′C=135°,∠APB=∠BP′C=135°;
(2)过点B作BE⊥BP,且BE=BP,连接PE、CE、AC,则PE=
=2
.
∵∠ABC=90°=∠PBE,
∴∠ABP=∠CBE.
∵AB=BC,BP=BE,
在△ABP与△CBE中,
∵
,
∴△ABP≌△CBE(SAS),
∴∠APB=∠CEB,CE=PA=1.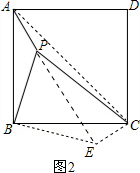
∵PE2+CE2=9=PC2,
∴∠PEC=90°,
∴∠APB=∠CEB=135°,
∴∠APE=∠APB+∠BPE=180°,
∴A、P、E三点共线,
∴AE=PA+PE=1+2
,
∴S△ACE=
AE•CE=
,S△PBE=
PB•BE=2,
∴S△ABC=S△PAB+S△PBC+S△PAC
=S△EBC+S△PBC+S△PAC
=S△PBE+S△ACE
=
,
∴S正方形ABCD=2S△ABC=5+2
.
 (1)如图1,将△ABP绕点B按顺时针方向旋转90°,使AB与BC重合;
(1)如图1,将△ABP绕点B按顺时针方向旋转90°,使AB与BC重合;则∠PBP′=90°,BP′=BP=2,P′C=PA=1;
由勾股定理得:PP′2=22+22=8;
∵P′C2=12=1,PC2=32=9,
∴PC2=PP′2+P′C2,
∴∠PP′C=90°;而∠BP′P=45°,
∴∠BP′C=135°,∠APB=∠BP′C=135°;
(2)过点B作BE⊥BP,且BE=BP,连接PE、CE、AC,则PE=
| BP2+BE2 |
| 2 |
∵∠ABC=90°=∠PBE,
∴∠ABP=∠CBE.
∵AB=BC,BP=BE,
在△ABP与△CBE中,
∵
|
∴△ABP≌△CBE(SAS),
∴∠APB=∠CEB,CE=PA=1.

∵PE2+CE2=9=PC2,
∴∠PEC=90°,
∴∠APB=∠CEB=135°,
∴∠APE=∠APB+∠BPE=180°,
∴A、P、E三点共线,
∴AE=PA+PE=1+2
| 2 |
∴S△ACE=
| 1 |
| 2 |
1+2
| ||
| 2 |
| 1 |
| 2 |
∴S△ABC=S△PAB+S△PBC+S△PAC
=S△EBC+S△PBC+S△PAC
=S△PBE+S△ACE
=
5+2
| ||
| 2 |
∴S正方形ABCD=2S△ABC=5+2
| 2 |
看了如图,P是正方形ABCD内的一...的网友还看了以下:
1.n阶方阵,A,B满足AB=A+B,且A-E可逆,求(A-E)^-1=2.如果2阶矩阵A的特征值 2020-04-12 …
设a={12},则A的特征值是()323设a={12},则A的特征值是()32A.l,2B.1,- 2020-04-13 …
设A是n阶矩阵A^2=E,证明r(A+E)+r(A-E)=n,的一步证明过程不懂由A^2=E,得A 2020-05-14 …
关于向量数量积的一些结论是怎么推出来的?⑴a⊥b等价于a·b=0⑵当a与b同向时,a·b=ㄧaㄧㄧ 2020-05-14 …
matlab 程序出错,帮我看看错在哪儿了函数function dvdt=huxi(t,v) gl 2020-05-16 …
定义,a是不为一的有理数我们把一减a分之一称为a的差,报数,如果二的差倒数是一减二分之一等于负一, 2020-05-16 …
下列符号代表精子的染色体组成 a与a'是一对同源染色体 其余以此类推 下列哪四个精子来自同一个精原 2020-05-17 …
1.在△ABC和△A'B'C'中,如果∠A=44°15′,∠B=67°12′,∠C=68°33′, 2020-06-03 …
1.要画一个三角形,需要知道三个元素,其中至少一个元素是2.三角形的三边长a,b,c,满足b分之a 2020-06-08 …
有难度M{A,B,C}==(A+B+C)/3m{A,B,C}=A(A为三数中最小的一个)则若M{A 2020-06-13 …