已知：线段AB．（1）尺规作图：作线段AB的垂直平分线l，与线段AB交于点D；（保留作图痕迹，不写作法）（2）在（1）的基础上，点C为l上一个动点（点C不与点D重合），连接CB，过点A作AE⊥B

Question

已知：线段AB．

（1）尺规作图：作线段AB的垂直平分线l，与线段AB交于点D；（保留作图痕迹，不写作法）
（2）在（1）的基础上，点C为l上一个动点（点C不与点D重合），连接CB，过点A作AE⊥BC，垂足为点E．
①当垂足E在线段BC上时，直接写出∠ABC度数的取值范围．
②请你画出一个垂足E在线段BC延长线上时的图形，并求证∠BAE=∠BCD．

Answer 1

（1）直线l即为所求作的直线．（见图1）

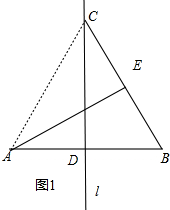
（2）①45°≤∠ABC<90°．
理由如下：连接AC，
当∠ACB≤90°时垂足E在线段BC上，
∵CD垂直平分AB，
∴CA=CB，
∴∠CAB=∠CBA，
∵2∠CBA+∠ACB=180°，
∴2∠CBA≥90°
∴∠CBA≥45°
∵∠CBA是锐角，
∴45°≤∠CBA<90°
②在图2中，


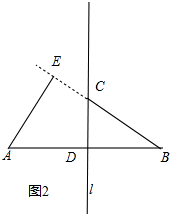
证明：∵线段AB的垂直平分线为l，
∴CD⊥AB，
∵AE⊥BE，
∴∠AEB=∠BDC=90°，
∴∠BAE+∠B=∠BCD+∠B=90°，
∴∠BAE=∠BCD．