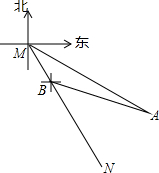
如图，东站枢纽建设要新建一条从M地到N地的公路，测得N点位于M点的南偏东30°，A点位于M点的南偏东60°，以A点为中心，半径为500米的圆形区域为文物保护区，又在B点测得BA的方向为南偏东7

Question

如图，东站枢纽建设要新建一条从M地到N地的公路，测得N点位于M点的南偏东30°，A点位于M点的南偏东60°，以A点为中心，半径为500米的圆形区域为文物保护区，又在B点测得BA的方向为南偏东75°，量得MB=400米，请计算后回答公路是否会穿越文物保护区（参考数据：√(3)≈1.732，√(2)≈1.414）

Answer 1

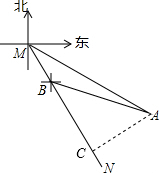过A作AC⊥BN于C，
由题意得∠CMA=30°，∠CBA=75°-30°=45°，MB=400m，
设AC=xm，
在Rt△AMC中，(AC)/(MC)=tan300=(√(3))/(3)，MC=√(3)x，
所以BC=MC-MB=√(3)x-400，
在Rt△ABC中，(AC)/(BC)=1，
∴√(3)x-400=x，
∴x=(400)/(√(3)-1)=200(√(3)+1)≈200(1.732+1)=546.4(m)，
因为AC=546.4m>500m，
所以公路不会穿过文物保护区．