在△ABC中，AB=AC，∠ABC=90°，D为AC中点，点P是线段AD上的一点，点P与点A、点D不重合），连接BP．将△ABP绕点P按顺时针方向旋转α角（0°<α<180°），得到△A1B1P，连接A1B1、BB1（1）如图①，

Question

在△ABC中，AB=AC，∠ABC=90°，D为AC中点，点P是线段AD上的一点，点P与点A、点D不重合），连接BP．将△ABP绕点P按顺时针方向旋转α角（0°<α<180°），得到△A₁B₁P，连接A₁B₁、BB₁
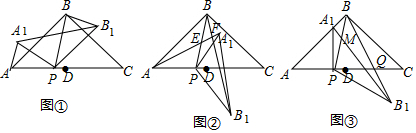
（1）如图①，当0°<α<90°，在α角变化过程中，请证明∠PAA₁=∠PBB₂．
（2）如图②，直线AA₁与直线PB、直线BB₁分别交于点E，F．设∠ABP=β，当90°<α<180°时，在α角变化过程中，是否存在△BEF与△AEP全等？若存在，求出α与β之间的数量关系；若不存在，请说明理由；
（3）如图③，当α=90°时，点E、F与点B重合．直线A₁B与直线PB相交于点M，直线BB_′与AC相交于点Q．若AB=√(2)，设AP=x，求y关于x的函数关系式．

Answer 1

（1）∵将△ABP绕点P按顺时针方向旋转α角（0°<α<180°），得到△A1B1P，∴∠APA1=∠BPB1=α，AP=A1P，BP=B1P，∴∠AA1P=∠A1AP=180°-∠APA12=180°-α2，∠BB1P=∠B1BP=180°-∠BPB12=180°-α2，∴∠PA...