如图，在?ABCD中，对角线AC、BD相交于点O，作∠BAD和∠BCD的平分线，分别交BD于点G、H，延长AG交BC于点E，延长CH交AD于点F．（1）求证：△ABG≌△CDH；（2）若∠BAE=2∠EAC，试判断四边形AE

Question

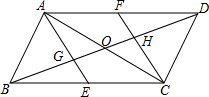如图，在?ABCD中，对角线AC、BD相交于点O，作∠BAD和∠BCD的平分线，分别交BD于点G、H，延长AG交BC于点E，延长CH交AD于点F．
（1）求证：△ABG≌△CDH；
（2）若∠BAE=2∠EAC，试判断四边形AECF是怎样的特殊四边形，并加以证明．

Answer 1

考点：
平行四边形的性质 全等三角形的判定与性质
专题：

分析：
（1）由在?ABCD中，可得AB∥CD，AB=CD，∠BAD=∠BCD，又由对角线AC、BD相交于点O，作∠BAD和∠BCD的平分线，分别交BD于点G、H，延长AG交BC于点E，延长CH交AD于点F，可得∠BAG=∠DCH，则可证得：△ABG≌△CDH；（2）易证得△ABE≌△CDF（ASA），继而可得四边形AECF是平行四边形，然后由∠BAE=2∠EAC，可得∠EAC=∠CAF，继而证得AE=CE，则可得四边形AECF是菱形．

（1）证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∠BAD=∠BCD，∴∠ABG=∠CDH，∵AG，CH分别是∠BAD和∠BCD的平分线，∴∠BAG=12∠BAD，∠DCH=12∠BCD，∴∠BAG=∠DCH，在△ABG和△CDH中，∠BAG=∠DCHAB=CD∠ABG=∠CDH，∴△ABG≌△CDH（ASA）；（2）四边形AECF是菱形．理由：∵AG平分∠BAD，∴∠BAE=∠DAE，∵∠BAE=2∠EAC，∴∠DAE=2∠EAC，∴∠EAC=∠FAC，在△ABE和△CDF中，∠BAG=∠DCFAB=CD∠ABE=∠CDF，∴△ABE≌△CDF（ASA），∴BE=DF，∵?ABCD中，AD∥BC，AD=BC，∴AF=CE，∴四边形AECF是平行四边形，∴∠ACE=∠CAF，∴∠ACE=∠CAE，∴AE=EC，∴四边形AECF是菱形．
点评：
此题考查了平行四边形的判定与性质以及全等三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．