早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,G为AB边的中点,∠BAD的平分线交DG于M,过点B作BE⊥BD交DG的延长线于点E,再过点A作AF⊥DG,交BC边于点F,交BD边于点N.(1)求证:AM=BN;(2)求证:AN=2EG;(3)连接MN
题目详情
如图,在正方形ABCD中,G为AB边的中点,∠BAD的平分线交DG于M,过点B作BE⊥BD交DG的延长线于点E,再过点A作AF⊥DG,交BC边于点F,交BD边于点N.
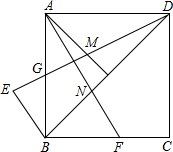
(1)求证:AM=BN;
(2)求证:AN=2EG;
(3)连接MN,若正方形ABCD的边长为2,求MN的长.

(1)求证:AM=BN;
(2)求证:AN=2EG;
(3)连接MN,若正方形ABCD的边长为2,求MN的长.
▼优质解答
答案和解析
证明:(1)∵正方形ABCD,
∴AB=AD,∠ABF=∠DAG=90°,
∵AF⊥DG,
∴∠BAF+∠AGD=90°,
∵∠AGD+∠ADG=90°,
∴∠BAF=∠ADG,
在△ADG与△BAF中,
,
∴△ADG≌△BAF(AAS),
∴∠BAG=∠ADM,
∵∠ABN=∠DAM=45°,AB=AD,
在△ABN与△DAM中
,
∴△ABN≌△DAM(AAS),
∴AM=BN,DM=AN;
(2)连接AE,如图:
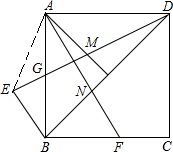
∵∠GAM=∠GBE=45°,∠AGM=∠BGE,AG=BG,
∴△BEG≌△AGM(ASA),
∴GM=GE,AM=BE,
∵∠ABE=∠DAM=45°,BE=AM,AB=AD,
∴△ABE≌△DAM,
∴∠BAE=∠ADM,DM=AE,
∴∠EAM=∠EAB+45°=∠ADM+45°=∠AME,
∴AE=ME,
∴AN=DM=AE=2GM;
(3)连接MN,如图3
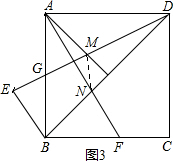
∵∠ADN=∠NBF,∠BNF=∠AND,
∴△ADN~△FBN,
∴
=
=
,
由(2)得:
=
,
∴
=
=
,
∵∠MDN=∠GDB,
∴△MDN∽△GDB,
∴
=
,
∴MN=
BG=
.
∴AB=AD,∠ABF=∠DAG=90°,
∵AF⊥DG,
∴∠BAF+∠AGD=90°,
∵∠AGD+∠ADG=90°,
∴∠BAF=∠ADG,
在△ADG与△BAF中,
|
∴△ADG≌△BAF(AAS),
∴∠BAG=∠ADM,
∵∠ABN=∠DAM=45°,AB=AD,
在△ABN与△DAM中
|
∴△ABN≌△DAM(AAS),
∴AM=BN,DM=AN;
(2)连接AE,如图:

∵∠GAM=∠GBE=45°,∠AGM=∠BGE,AG=BG,
∴△BEG≌△AGM(ASA),
∴GM=GE,AM=BE,
∵∠ABE=∠DAM=45°,BE=AM,AB=AD,
∴△ABE≌△DAM,
∴∠BAE=∠ADM,DM=AE,
∴∠EAM=∠EAB+45°=∠ADM+45°=∠AME,
∴AE=ME,
∴AN=DM=AE=2GM;
(3)连接MN,如图3

∵∠ADN=∠NBF,∠BNF=∠AND,
∴△ADN~△FBN,
∴
| DN |
| BN |
| AD |
| BF |
| 2 |
| 1 |
由(2)得:
| DM |
| GM |
| 2 |
| 1 |
∴
| DN |
| BD |
| DM |
| DG |
| 2 |
| 3 |
∵∠MDN=∠GDB,
∴△MDN∽△GDB,
∴
| MN |
| BG |
| 2 |
| 3 |
∴MN=
| 2 |
| 3 |
| 2 |
| 3 |
看了如图,在正方形ABCD中,G为...的网友还看了以下:
直角三角形中,两条直角边a,b和斜边c之间满足下面的关系:a2+b2=c2.如果一个直角三角形的斜 2020-05-13 …
如图所示,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,BG=10只要初一 2020-05-16 …
一只老鼠沿着长方形A-B-C的方向逃跑,同时一只猫也从A点出发沿着A-D-C的方向追捕老鼠.结果在 2020-05-17 …
一只老鼠沿着长方形A→B→C的方向逃跑,同时一只猫也从A点出发沿着A→D→C方向追捕老鼠,结果在B 2020-05-17 …
一只老鼠沿着平行四边形ADC同时一只猫也从A点出发沿ABC的方向捉老鼠结果在DC边上的E点捉住老鼠 2020-05-17 …
一只老鼠沿着平行四边形ADC同时一只猫也从A点出发沿ABC的方向捉老鼠结果在DC边上的E点捉住老鼠 2020-05-17 …
如右图所示,一只老鼠沿着平行四边形ADC方向逃跑:同时,一只猫也从A出发沿着ABC的方向抓捕老鼠. 2020-05-17 …
如图所示,在RT三角形ABC中,角C=90度,AC=4厘米,BC=3厘米,把三角形ABC沿BD折叠 2020-05-23 …
如图,矩形纸片ABCD,AB=3,AD=5,折叠纸片,使点A落在BC边上的E处,折痕为PQ,当点E 2020-06-12 …
(2014•武昌区模拟)如图所示的直角三角形ABC是玻璃砖的横截面,∠B=90°,∠A=30°E为 2020-06-19 …