早教吧作业答案频道 -->数学-->
已知:在▱ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD于F,过点D作DG⊥AE于G,延长DG交BC于H(1)如图1,若点E与点C重合,且AF=5,求AD的长;(2)如图2,连接FH,求证:∠AFB=∠HFB;(3)
题目详情
已知:在▱ABCD中,∠BAD=45°,AB=BD,E为BC上一点,连接AE交BD于F,过点D作DG⊥AE于G,延长DG交BC于H
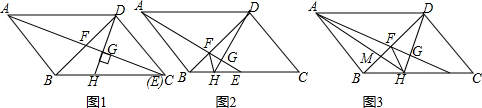
(1)如图1,若点E与点C重合,且AF=
,求AD的长;
(2)如图2,连接FH,求证:∠AFB=∠HFB;
(3)如图3,连接AH交BF于M,当M为BF的中点时,请直接写出AF与FH的数量关系.

(1)如图1,若点E与点C重合,且AF=
| 5 |
(2)如图2,连接FH,求证:∠AFB=∠HFB;
(3)如图3,连接AH交BF于M,当M为BF的中点时,请直接写出AF与FH的数量关系.
▼优质解答
答案和解析
(1) 如图1中,∵AB=BD,∠BAD=45°,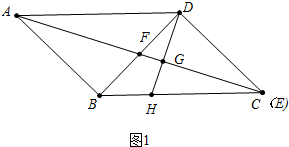
∴∠BDA=∠BAD=45°,
∴∠ABD=90°,
∵四边形ABCD是平行四边形,
∴E、C重合时BF=
BD=
AB,
在RT△ABF中,∵AF2=AB2+BF2,
∴(
)2=(2BF)2+BF2,
∴BF=1,AB=2,
在RT△ABD中,AD=
=2
.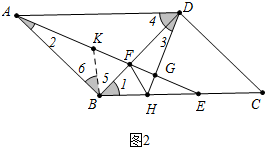
(2)证明:如图2中,在AF上截取AK=HD,连接BK,
∵∠AFD=∠ABF+∠2=∠FGD+∠3,∠ABF=∠FGD=90°,
∴∠2=∠3,
在ABK和△DBH中,
,
∴△ABK≌△DBH,
∴BK=BH,∠6=∠1,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠4=∠1=∠6=45°,
∴∠5=∠ABD-∠6=45°,
∴∠5=∠1,
在△FBK和△FBH中,
,
∴△FBK≌△FBH,
∴∠BFK=∠BFH.
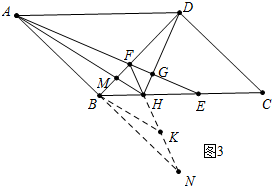
(3)结论AF=3FH.
理由:如图3中,延长FH、AB交于点N,作BK∥AH交FN于K.
∵∠AFB+∠BAF=90°,∠BFN+∠N=90°,∠BFN=∠BFA,
∴∠FAB=∠N,
∴FA=FN,
∵FB⊥AN,
∴AB=BN,
∵BK∥AH,
∴HK=KN,
∵FM=BM,MH∥BK,
∴FH=HK,
∴FH=HK=FN.
∴FN=3FH,
∵AF=FN,
∴AF=3FH.

∴∠BDA=∠BAD=45°,
∴∠ABD=90°,
∵四边形ABCD是平行四边形,
∴E、C重合时BF=
| 1 |
| 2 |
| 1 |
| 2 |
在RT△ABF中,∵AF2=AB2+BF2,
∴(
| 5 |
∴BF=1,AB=2,
在RT△ABD中,AD=
| AB2+BD2 |
| 2 |

(2)证明:如图2中,在AF上截取AK=HD,连接BK,
∵∠AFD=∠ABF+∠2=∠FGD+∠3,∠ABF=∠FGD=90°,
∴∠2=∠3,
在ABK和△DBH中,
|
∴△ABK≌△DBH,
∴BK=BH,∠6=∠1,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠4=∠1=∠6=45°,
∴∠5=∠ABD-∠6=45°,
∴∠5=∠1,
在△FBK和△FBH中,
|

∴△FBK≌△FBH,
∴∠BFK=∠BFH.
(3)结论AF=3FH.
理由:如图3中,延长FH、AB交于点N,作BK∥AH交FN于K.
∵∠AFB+∠BAF=90°,∠BFN+∠N=90°,∠BFN=∠BFA,
∴∠FAB=∠N,
∴FA=FN,
∵FB⊥AN,
∴AB=BN,
∵BK∥AH,
∴HK=KN,
∵FM=BM,MH∥BK,
∴FH=HK,
∴FH=HK=FN.
∴FN=3FH,
∵AF=FN,
∴AF=3FH.
看了已知:在▱ABCD中,∠BAD...的网友还看了以下:
设函数f(x)在x=a的某个邻域内有定义,则f(x)在x=a处可导的一个充分条件是?请写出分析过程! 2020-03-30 …
A.F,H,C,D,P,A,M,Q,R,S,Y,XB.P,A,C,S,Q,D,F,X,R,H,M,Y 2020-05-26 …
设一组初始记录关键字序列为(Q,H,C,Y,P,A,M,S,R,D,F,X),则按字母升序的第一趟 2020-07-17 …
关于导数的一个问题设f(x)在x=a的某个领域内有定义,则f(x)在x=a处可导的一个充分条件是: 2020-07-23 …
一道高数题目设f(x)在x=a的某个临域内有定义,则f(x)在x=a处可导的一个充分条件是()(A 2020-07-30 …
设f(x)在x=a的某个邻域内有定义,则f(x)在x=a处可导的一个充分条件是()A.limh→+ 2020-07-31 …
设f(x)在x=a的某个邻域内有定义,则f(x)在x=a处可导的一个充分条件是()A.limh→+ 2020-07-31 …
设f(x)在x=a的某个邻域内有定义,则f(x)在x=a处可导的一个充分条件是()A.limh→+ 2020-07-31 …
f(x)在x=a的某个领域内有定义,则他在x=a处可导的一个充分条件是当h趋于0,lin[f(a+ 2020-07-31 …
下图为水循环示意图,读图回答题。1.能正确反映海陆间水循环过程的是2.水循环中的A.a→f→h→gB 2020-12-03 …