早教吧作业答案频道 -->数学-->
如图1,在矩形ABCD中,点E为边AD上靠近D的三等分点,点F为边CD的中点,AB=AE=4,现将△ABE沿BE边折至△PBE位置,且平面PBE⊥平面BCDE.(Ⅰ)求证:平面PBE⊥平面PEF;(Ⅱ)求四棱锥P-BCFE的体
题目详情
如图1,在矩形ABCD中,点E为边AD上靠近D的三等分点,点F为边CD的中点,AB=AE=4,现将△ABE沿BE边折至△PBE位置,且平面PBE⊥平面BCDE.
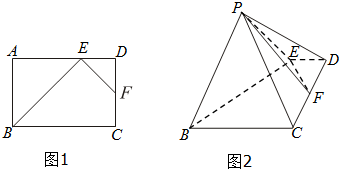
(Ⅰ)求证:平面PBE⊥平面PEF;
(Ⅱ)求四棱锥P-BCFE的体积.

(Ⅰ)求证:平面PBE⊥平面PEF;
(Ⅱ)求四棱锥P-BCFE的体积.
▼优质解答
答案和解析
(1)证明:∵点E为边AD上靠近D的三等分点,点F为边CD的中点,AB=AE=4,
∴AB=AE=
AD=4,
∴DE=
AD=
AB=2,
∵F为CD边的中点,
∴DE=DF,又DE⊥DF,
∴∠DEF=45°,
同理∠AEB=45°,
∴∠BEF=45°,即EF⊥BE,
又平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE,
∴EF⊥平面PBE,
EF⊂平面PEF,
∴平面PBE⊥平面PEF;如图,
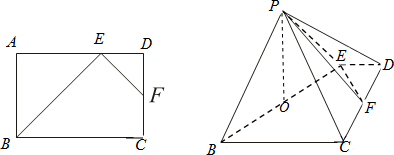 在Rt△DEF中,∵ED=DF,∴∠DEF=45°.
在Rt△DEF中,∵ED=DF,∴∠DEF=45°.
在Rt△ABE中,∵AE=AB,∴∠AEB=45°,
∴∠BEF=90°,则EF⊥BE.
∵平面PBE⊥平面BCDE,且平面PBE∩平面BCDE=BE,
∴EF⊥平面PBE,
∵EF⊂平面PEF,∴平面PBE⊥平面PEF;
(2) 过P做PO⊥BE,
∵PO⊂平面PBE,平面PBE⊥平面BCDE且平面PBE∩平面BCDE=BE,
∴PO⊥平面BCDE,
四棱锥P-BCFE的高h=PO=2
.
S四边形BCFE=S矩形ABCD-S△ABE-S△DEF=6×4-
×4×4-
×2×2=14,
则VP-BCFE=
S四边形BCFE•h=
×14×2
=
.
∴AB=AE=
| 2 |
| 3 |
∴DE=
| 1 |
| 3 |
| 1 |
| 2 |
∵F为CD边的中点,
∴DE=DF,又DE⊥DF,
∴∠DEF=45°,
同理∠AEB=45°,
∴∠BEF=45°,即EF⊥BE,
又平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE,
∴EF⊥平面PBE,
EF⊂平面PEF,
∴平面PBE⊥平面PEF;如图,
 在Rt△DEF中,∵ED=DF,∴∠DEF=45°.
在Rt△DEF中,∵ED=DF,∴∠DEF=45°.在Rt△ABE中,∵AE=AB,∴∠AEB=45°,
∴∠BEF=90°,则EF⊥BE.
∵平面PBE⊥平面BCDE,且平面PBE∩平面BCDE=BE,
∴EF⊥平面PBE,
∵EF⊂平面PEF,∴平面PBE⊥平面PEF;
(2) 过P做PO⊥BE,
∵PO⊂平面PBE,平面PBE⊥平面BCDE且平面PBE∩平面BCDE=BE,
∴PO⊥平面BCDE,
四棱锥P-BCFE的高h=PO=2
| 2 |
S四边形BCFE=S矩形ABCD-S△ABE-S△DEF=6×4-
| 1 |
| 2 |
| 1 |
| 2 |
则VP-BCFE=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
28
| ||
| 3 |
看了如图1,在矩形ABCD中,点E...的网友还看了以下:
在四棱台ABCD-A'B'C'D'中,他的下底面ABCD是边长为2的正方形,AA'垂直于底面ABCD 2020-03-30 …
平面直角坐标系中,OP 平分∠xoy,B 为 Y 轴正半轴上一点,D 为第四象限内一点,BD 交平 2020-05-16 …
平面直角坐标系中,OP平分∠xoy,B为Y轴正半轴上一点,D为第四象限内一点,BD交x轴于C,过D 2020-05-16 …
如图,一次函数y=-4x-4的图象与x轴、y轴分别交于A、C两点,抛物线y=43x2+bx+c的图 2020-06-12 …
如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP, 2020-06-19 …
已知:如图,二次函数的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9.(1)求 2020-07-15 …
已知四棱锥的底面是边长为的正方形,底面,、分别为棱、的中点.(1)求证:平面(2)已知二面角的余弦 2020-07-21 …
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)。(1)求抛物 2020-08-01 …
已知,抛物线y=﹣2分之一x²+2分之3+2与x轴交于A、B两点,与y轴交于C点.D为第四象限的抛物 2020-11-01 …
如图,已知抛物线与x轴交于A(-1,0)、E(5,0)两点,与y轴交于点B(0,5).(1)求抛物线 2021-01-10 …