早教吧作业答案频道 -->数学-->
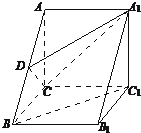
如图,三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1,D为AB的中点,且CD⊥DA1(I)求证:BC1∥平面DCA1(II)求证:平面ABC⊥平面ABB1A1(III)求BC1与平面ABB1A1所成角的大小.
题目详情
如图,三棱柱ABC-A1B1C1中,AC⊥BC,AB⊥BB1,AC=BC=BB1,D为AB的中点,且CD⊥DA1
(I)求证:BC1∥平面DCA1
(II)求证:平面ABC⊥平面ABB1A1
(III)求BC1与平面ABB1A1所成角的大小.
(I)求证:BC1∥平面DCA1
(II)求证:平面ABC⊥平面ABB1A1
(III)求BC1与平面ABB1A1所成角的大小.

▼优质解答
答案和解析
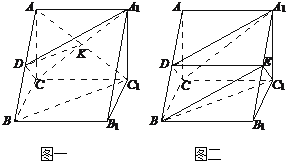
(I)证明:如图一,连接AC1与A1C交于点K,连接DK.
在△ABC1中,D、K为中点,∴DK∥BC1,
又DK⊂平面DCA1,BC1⊄平面DCA1,
∴BC1∥平面DCA1.
(II)证明:∵AC=BC,D为AB中点,
∴CD⊥AB,又CD⊥DA1,
∴CD⊥面AA1B1B,
又∵CD⊂平面ABC,∴平面A1B1B⊥平面ABC.
(III)取A1B1的中点E,又D为AB的中点,∴DE、BB1、CC1平行且相等,
∴DCC1E是平行四边形,∴C1E、CD平行且相等.
又CD⊥平面ABB1A1,∴C1E⊥平面ABB1A1,∴∠EBC1即所求角,
由前面证明知CD⊥平面ABB1A1,∴CD⊥BB1,
又AB⊥BB1,AB∩CD=D,∴BB1⊥平面ABC,∴此三棱柱为直棱柱.
设AC=BC=BB1=2,∴BC1=2
,EC1=
,∠EBC1=30°.
在△ABC1中,D、K为中点,∴DK∥BC1,
又DK⊂平面DCA1,BC1⊄平面DCA1,
∴BC1∥平面DCA1.

(II)证明:∵AC=BC,D为AB中点,
∴CD⊥AB,又CD⊥DA1,
∴CD⊥面AA1B1B,
又∵CD⊂平面ABC,∴平面A1B1B⊥平面ABC.
(III)取A1B1的中点E,又D为AB的中点,∴DE、BB1、CC1平行且相等,
∴DCC1E是平行四边形,∴C1E、CD平行且相等.
又CD⊥平面ABB1A1,∴C1E⊥平面ABB1A1,∴∠EBC1即所求角,
由前面证明知CD⊥平面ABB1A1,∴CD⊥BB1,
又AB⊥BB1,AB∩CD=D,∴BB1⊥平面ABC,∴此三棱柱为直棱柱.
设AC=BC=BB1=2,∴BC1=2
| 2 |
| 2 |
看了如图,三棱柱ABC-A1B1C...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
如果梯形的对角互补,最大角是最小角的3倍,上底为a,下底为b(b>a),则两底间的距离为A:a+b 2020-04-26 …
2014成都一诊数学第15题高中的东西这么多年过去全忘了直接来提问设⊙O为不等边△ABC的外接圆, 2020-06-22 …
设a,b,c∈R,证明a^2acc^23b(abc)≥0,并指出等号何时成立问题补充:证明:不妨设 2020-06-23 …
为了应用平方差公式计算(a-b+c)(a+b-c),必须先适当变形,下列各变形中,正确的是()A. 2020-07-31 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
已知抛物线y=x2-2bx+c(1)若抛物线的顶点坐标为(2,-3),求b,c的值;(2)若b+c= 2020-11-24 …
已知a+b+c=0,abc不等于0,且a,b,c,互不相等,求证:[(b-c)/a+(c-a)/b+ 2020-12-01 …
设a、b、c为实数,且a+b+c=2倍的(根号a+1)+4倍的(根号b+1)+b倍的(根号c-2)- 2020-12-31 …