早教吧作业答案频道 -->数学-->
在四边形ABCD中,AB=AD,∠B=∠D=90°,∠BCD=120°,现将一个30°角的顶点落在点A处.(1)如图①,当该角的两边分别与BC、CD边相交于E、F时.求证:EF=BE+DF;(2)现在将该角绕点A进行旋转,其
题目详情
在四边形ABCD中,AB=AD,∠B=∠D=90°,∠BCD=120°,现将一个30°角的顶点落在点A处.
(1)如图①,当该角的两边分别与BC、CD边相交于E、F时.求证:EF=BE+DF;
(2)现在将该角绕点A进行旋转,其两边分别与BC、CD边的延长线相交于点F,那么(1)中的结论是否仍然成立?若成立,说明理由;若不成立,试探究线段BE与DF之间的等量关系,并加以证明.(利用图②进行探索)
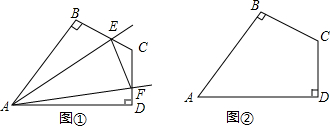
(1)如图①,当该角的两边分别与BC、CD边相交于E、F时.求证:EF=BE+DF;
(2)现在将该角绕点A进行旋转,其两边分别与BC、CD边的延长线相交于点F,那么(1)中的结论是否仍然成立?若成立,说明理由;若不成立,试探究线段BE与DF之间的等量关系,并加以证明.(利用图②进行探索)

▼优质解答
答案和解析
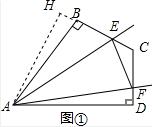 (1)如图①,
(1)如图①,
延长CB到H点,使BH=DF,连接AH,
∵∠B=∠D=90°,∠BCD=120°,
∴∠D+∠B=180°,
∵∠ABE+∠ABH=180°,
∴∠ABH=∠D,
∵AD=AB,BH=DF,
∴在△ABH和△ADF中,
,
∴△ABH≌△ADF(SAS),
∴AH=AF,∠HAB=∠FAD,
∵∠DAB=60°,∠FAE=30°,
∴∠FAD+∠BAE=30°,
∴∠BAE+∠HAB=30°,即∠HAE=30°,
在△HAE和△EAF中,
,
∴△HAE≌△FAE(SAS),
∴HE=EF,
∵HE=HB+BE=DF+BE,
∴EF=BE+DF;
(2)(1)中的结论不成立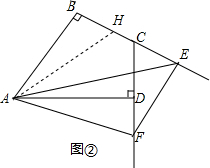 ,
,
如图②,在BC上截取BH=DF,
在△ABH与△ADF中,
,
∴△ABH≌△ADF,
∴∠BAH=∠DAF,AH=AF,
∴∠EAF=30°,
∴∠BAH+∠EAD=30°,
∵∠B=∠D=90°,∠BCD=120°,
∴∠BAD=60°,
∴∠HAE=30°,
在△HAE与△FAE中,
,
∴△HAE≌△FAE,
∴HE=EF,
∵BE=BH+HE,
∴BE=DF+EF.
 (1)如图①,
(1)如图①,延长CB到H点,使BH=DF,连接AH,
∵∠B=∠D=90°,∠BCD=120°,
∴∠D+∠B=180°,
∵∠ABE+∠ABH=180°,
∴∠ABH=∠D,
∵AD=AB,BH=DF,
∴在△ABH和△ADF中,
|
∴△ABH≌△ADF(SAS),
∴AH=AF,∠HAB=∠FAD,
∵∠DAB=60°,∠FAE=30°,
∴∠FAD+∠BAE=30°,
∴∠BAE+∠HAB=30°,即∠HAE=30°,
在△HAE和△EAF中,
|
∴△HAE≌△FAE(SAS),
∴HE=EF,
∵HE=HB+BE=DF+BE,
∴EF=BE+DF;
(2)(1)中的结论不成立
 ,
,如图②,在BC上截取BH=DF,
在△ABH与△ADF中,
|
∴△ABH≌△ADF,
∴∠BAH=∠DAF,AH=AF,
∴∠EAF=30°,
∴∠BAH+∠EAD=30°,
∵∠B=∠D=90°,∠BCD=120°,
∴∠BAD=60°,
∴∠HAE=30°,
在△HAE与△FAE中,
|
∴△HAE≌△FAE,
∴HE=EF,
∵BE=BH+HE,
∴BE=DF+EF.
看了在四边形ABCD中,AB=AD...的网友还看了以下:
A.0个B.1个C.1个或多个D.0个或多个 2020-05-26 …
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0). 2020-06-11 …
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0). 2020-06-11 …
1.一个三角形中,内角小于90度的角至少有A.1个B.2个C.3个D.0个2.满足条件∠A=∠B= 2020-06-12 …
如图所示,△ABC中,AD⊥BC于D,对于下列中的每一个条件①∠B+∠DAC=90∘;②∠B=∠DA 2020-11-02 …
过直线l外两点作与直线l平行的平面,可以作()A.1个B.1个或无数个C.0个或无数个D.0个、1个 2020-11-03 …
直线l外有两点A、B,若要在l上找一点,使这点与点A、B的距离相等,这样的点能找到()A.0个B.1 2020-11-06 …
一个池塘中,水蚤、虾、鲤鱼等所有动物集合起来组成()A.一个群落B.一个种群C.多个群落D.多个种群 2020-12-22 …
互不重合的三条直线的公共点的个数是()A.只可能是0个,1个或3个B.只可能是0个,1个或2个C.只 2020-12-31 …
某省去年上半年受企业效益下滑、农产品价格回落等因素的影响,城乡居民收入增长同比回落6.0个和7.6个 2021-01-24 …