早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=2∠B,∠BAC的平分线AD交BC于D,过C作CN⊥AD交AD于H,交AB于N.(1)求证:△ANC为等腰三角形;(2)试判断BN与CD的数量关系,并说明理由.
题目详情
如图,在△ABC中,∠ACB=2∠B,∠BAC的平分线AD交BC于D,过C作CN⊥AD交AD于H,交AB于N.
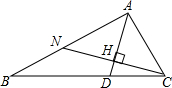
(1)求证:△ANC为等腰三角形;
(2)试判断BN与CD的数量关系,并说明理由.

(1)求证:△ANC为等腰三角形;
(2)试判断BN与CD的数量关系,并说明理由.
▼优质解答
答案和解析
(1)证明:∵CN⊥AD,
∴∠AHN=∠AHC=90°,
又∵AD平分∠BAC,
∴∠NAH=∠CAH,
又∵在△ANH和△ACH中
∠AHN+∠NAH+∠ANH=180°,∠AHC+∠CAH+∠ACH=180°
∴∠ANH=∠ACH,
∴AN=AC,
∴△ANC为等腰三角形;
(2) BN=CD,
原因如下:如图:连接ND
∵△AND和△ACD中
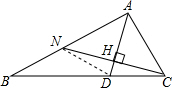
∴△AND≌△ACD(ASA),
∴DN=DC,∠AND=∠ACD,
又∵∠ACB=2∠B,
∴∠AND=2∠B
又∵△BND中,∠AND=∠B+∠NDB,
∴∠B=∠NDB,
∴NB=ND,
∴BN=CD.
∴∠AHN=∠AHC=90°,
又∵AD平分∠BAC,
∴∠NAH=∠CAH,
又∵在△ANH和△ACH中
∠AHN+∠NAH+∠ANH=180°,∠AHC+∠CAH+∠ACH=180°
∴∠ANH=∠ACH,
∴AN=AC,
∴△ANC为等腰三角形;
(2) BN=CD,
原因如下:如图:连接ND
∵△AND和△ACD中

|
∴△AND≌△ACD(ASA),
∴DN=DC,∠AND=∠ACD,
又∵∠ACB=2∠B,
∴∠AND=2∠B
又∵△BND中,∠AND=∠B+∠NDB,
∴∠B=∠NDB,
∴NB=ND,
∴BN=CD.
看了如图,在△ABC中,∠ACB=...的网友还看了以下:
急,明天要交,如图,一扇窗是由一个直径为d的半圆和一个高为h的长方形组成(1)若窗框长度总和为20 2020-05-13 …
如图(1)所示,称“对顶三角形”,其中,∠A+∠B=∠C+∠D,利用这个结论,完成下列填空.①如图 2020-06-13 …
如图,等腰直角△ABC内接于⊙O,D为⊙O上一点,连接AD、BD、CD(1)如图(1),点D在半圆 2020-06-13 …
如图(1)所示,称“对顶三角形”其中∠A+∠B=∠C+∠D,利用这个结论,完成下列填空.①如图(2 2020-06-30 …
如果a,b,c,d是不为0的整数满足1/a+1/b=1/c1/b+1/c=1/d1/c+1/d=1 2020-07-09 …
从动量定理到动能定理的推理中的一个问题推理过程如下ma=d(mv)/dt[d(mv)/dt]*vd 2020-07-13 …
vim如何用正则表达式把数字换成相同长度的空格呢?比如如下1.23451.21.32.32.123 2020-07-23 …
设整数m>=2,如果有一个整数,使得(a,m)的最大公约数等于d,d=1,那么...设整数m>=2, 2020-11-18 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …
如果a、b、c、d都是不为零的整数,且1/a+1/b=1/c,1/b+1/c=1/d,1/c+1/d 2021-02-01 …