早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.(1)求证:AD=AF;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
题目详情
如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
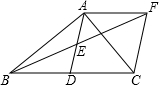
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
▼优质解答
答案和解析
(1)证明:∵AF∥BC,
∴∠EAF=∠EDB,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(ASA),
∴AF=BD,
∵在△ABC中,∠BAC=90°,AD是中线,
∴AD=BD=DC=
BC,
∴AD=AF;
(2) 四边形ADCF是正方形.
∵AF=BD=DC,AF∥BC,
∴四边形ADCF是平行四边形,
∵AB=AC,AD是中线,
∴AD⊥BC,
∵AD=AF,
∴四边形ADCF是正方形.
∴∠EAF=∠EDB,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
|
∴△AEF≌△DEB(ASA),
∴AF=BD,
∵在△ABC中,∠BAC=90°,AD是中线,
∴AD=BD=DC=
| 1 |
| 2 |
∴AD=AF;
(2) 四边形ADCF是正方形.
∵AF=BD=DC,AF∥BC,
∴四边形ADCF是平行四边形,
∵AB=AC,AD是中线,
∴AD⊥BC,
∵AD=AF,
∴四边形ADCF是正方形.
看了如图,在△ABC中,∠BAC=...的网友还看了以下:
求解几道不等式证明1.求证:x²>4x—5.2.求证:a的四次方+1≥a的三次方+a3.已知a>0 2020-04-27 …
直接证明与间接证明1:已知非零向量a,b,且相互垂直,求证:[/a/﹢/b/]÷﹙/a-b/﹚≤√ 2020-07-05 …
数学厉害的进来1求证a²+3b²≥2b(a+b)2,求证a²+b²+2≥2a+2b3,已知a≠2, 2020-07-09 …
在用反证法证明命题“已知a,b,c∈(0,2),求证a(2-b),b(2-c),c(2-a)不可能 2020-07-16 …
(1/2)已知an=(1+根号下2)的n次方(n属于N*)若an=a+b根号下2(a.b属于Z)求 2020-07-30 …
比较法证明不等式可分为作差比较法和作商比较法:(1)要证明a>b,只要证明;要证a<b,只要证明. 2020-08-01 …
a是x2+x+1=0方程的根求证a不是实数反证法a是x2+x+1=0方程的根求证a不是实数用反证法 2020-08-01 …
求一不等式证明.已知:x,y,z>=0,x+y+z=6.求证:(x+1/x)(y+1/y)(z+1/ 2020-10-31 …
已知abc两两相互独立,求证P(a交b交c)=p(a)p(b)p(c)已知ab相互独立,求证a已知a 2020-12-01 …
直接证明与间接证明1:已知非零向量a,b,且相互垂直,求证:[/a/﹢/b/]÷﹙/a-b/﹚≤√2 2020-12-07 …