早教吧作业答案频道 -->数学-->
如图1,菱形ABCD中,∠BAD=60°,点E、F分别是边AB、AD上两个动点,满足AE=DF,连接BF与DE相交于点G.(1)如图2,连接BD,求∠BGD的度数;(2)如图3,作CH⊥BG于H点,求证:2GH=DG+BG.
题目详情
如图1,菱形ABCD中,∠BAD=60°,点E、F分别是边AB、AD上两个动点,满足AE=DF,连接BF与DE相交于点G.
(1)如图2,连接BD,求∠BGD的度数;
(2)如图3,作CH⊥BG于H点,求证:2GH=DG+BG.
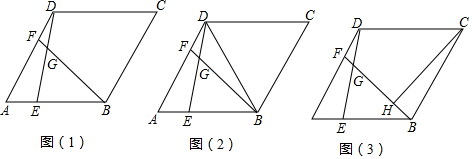
(1)如图2,连接BD,求∠BGD的度数;
(2)如图3,作CH⊥BG于H点,求证:2GH=DG+BG.

▼优质解答
答案和解析
(1) 如图2中,
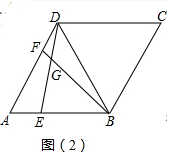
∵四边形ABCD是菱形,
∴AD=AB,
∵∠A=60°,
∴△ABD是等边三角形,
∴AB=DB,∠A=∠FDB=60°,
在△DAE和△BDF中,
,
∴△DAE≌△BDF,
∴∠ADE=∠DBF,
∵∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,
∴∠BGD=180°-∠BGE=120°.
(2)证明:如图3中,延长GE到M,使得GM=GB,连接BD、CG.
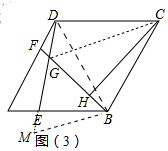
∵∠MGB=60°,GM=GB,
∴△GMB是等边三角形,
∴∠MBG=∠DBC=60°,
∴∠MBD=∠GBC,
在△MBD和△GBC中,
,
∴△MBD≌△GBC,
∴DM=GC,∠M=∠CGB=60°,
∵CH⊥BG,
∴∠GCH=30°,
∴CG=2GH,
∵CG=DM=DG+GM=DG+GB,
∴2GH=DG+GB.

∵四边形ABCD是菱形,
∴AD=AB,
∵∠A=60°,
∴△ABD是等边三角形,
∴AB=DB,∠A=∠FDB=60°,
在△DAE和△BDF中,
|
∴△DAE≌△BDF,
∴∠ADE=∠DBF,
∵∠EGB=∠GDB+∠GBD=∠GDB+∠ADE=60°,
∴∠BGD=180°-∠BGE=120°.
(2)证明:如图3中,延长GE到M,使得GM=GB,连接BD、CG.

∵∠MGB=60°,GM=GB,
∴△GMB是等边三角形,
∴∠MBG=∠DBC=60°,
∴∠MBD=∠GBC,
在△MBD和△GBC中,
|
∴△MBD≌△GBC,
∴DM=GC,∠M=∠CGB=60°,
∵CH⊥BG,
∴∠GCH=30°,
∴CG=2GH,
∵CG=DM=DG+GM=DG+GB,
∴2GH=DG+GB.
看了如图1,菱形ABCD中,∠BA...的网友还看了以下:
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
现有A,B,C,D,E,F,G七种短周期主族元素,原子序数依次增大.已知A与D,C与F分别同主族, 2020-07-07 …
(A+B+C+D)^4=?(A+B+C+D+E)^5=?(A+B+C+D+E+F)^6=?(A+B 2020-07-18 …
求证:(1)b=d,f=b^2;(2)求a,b,c,d,e,f,g的值(题目如下)设a、b、c、d 2020-07-27 …
(x-3)6=ax6+bx5+cx4+dx3+ex2+fx+g(其中数字为x的次数)求a+b+c+ 2020-07-30 …
EXCEL循环或计算问题。F=A+B+C+D+E。(A.B.C.D.E.F.均要大于零)E=A*10 2020-11-01 …
sql自定义求和函数与计算列的用法做一个分数统计表,列a,b,c,d,e,f,其sql自定义求和函数 2020-11-08 …
绕弯的题,我被绕晕了,求函数有七组数据,ABCDEFG,已知A,B,C,七组数据的关系D+E=B,F 2020-11-11 …
将若干个数a1,a2,a3.的最大值和最小值分别记max(a1,a2,a3.)和min(a1,a2, 2020-12-07 …
求解多元一次不等式的编程47a-b-c-d-e-f-g>047b-a-c-d-e-f-g>023c- 2020-12-14 …