早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,二次函数图象所在的位置如图所示:(1)请根据图象信息求该二次函数的表达式;(2)将该图象(x>0)的部分,沿y轴翻折得到新的图象,请直接写出翻折后的二
题目详情
在平面直角坐标系xOy中,二次函数图象所在的位置如图所示:
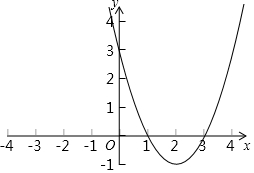
(1)请根据图象信息求该二次函数的表达式;
(2)将该图象(x>0)的部分,沿y轴翻折得到新的图象,请直接写出翻折后的二次函数表达式;
(3)在(2)的条件下与原有二次函数图象构成了新的图象,记为图象G,现有一次函数 y=
x+b的图象与图象G有4个交点,请画出图象G的示意图并求出b的取值范围.

(1)请根据图象信息求该二次函数的表达式;
(2)将该图象(x>0)的部分,沿y轴翻折得到新的图象,请直接写出翻折后的二次函数表达式;
(3)在(2)的条件下与原有二次函数图象构成了新的图象,记为图象G,现有一次函数 y=
| 2 |
| 3 |
▼优质解答
答案和解析
(1)由图象可知抛物线经过点(1,0),(3,0),(0,3),
设抛物线的解析式为y=a(x-1)(x-3),
代入(0,3)得,3a=3,
解得a=1,
∴y=(x-1)(x-3),
即:y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∵顶点为(2,-1),
∴沿y轴翻折得到新的图象顶点为(-2,-1),
∴翻折后的二次函数表达式y=x2+4x+3(x<0);
(3)示意图正确
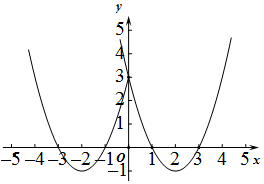
解x2+4x+3=
x+b
整理得:x2+
x+3-b=0
∵△=(
)2-4×1•(3-b)>0
解得:b>
,
当y=
x+b过(0,3)时,b=3,
所以综上所述符合题意的b的取值范围是
<b<3.
设抛物线的解析式为y=a(x-1)(x-3),
代入(0,3)得,3a=3,
解得a=1,
∴y=(x-1)(x-3),
即:y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∵顶点为(2,-1),
∴沿y轴翻折得到新的图象顶点为(-2,-1),
∴翻折后的二次函数表达式y=x2+4x+3(x<0);
(3)示意图正确
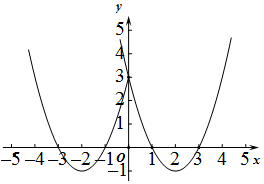
解x2+4x+3=
| 2 |
| 3 |
整理得:x2+
| 10 |
| 3 |
∵△=(
| 10 |
| 3 |
解得:b>
| 2 |
| 9 |
当y=
| 2 |
| 3 |
所以综上所述符合题意的b的取值范围是
| 2 |
| 9 |
看了在平面直角坐标系xOy中,二次...的网友还看了以下:
一个二次函数,其图象由抛物线y=1/2x^2向右平移一个单位,再向上平移k个单位(k>0)得到,平 2020-04-26 …
函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1) 2020-05-02 …
对于函数y=5/x,当x<0时,y0,这部分图像在第几象限;对于函数y=-5/x,当x>0时,y0 2020-05-22 …
计算机图形学把通用球面在x方向放大2倍,在y方向放大3倍,然后饶z轴旋转30°,计算变换后图形的隐 2020-06-19 …
已知函数f(x)=Asin(wx+p)(A>0,w<0,|p|<π/2)的部分图像如图所示(1)求 2020-06-27 …
已知二次函数的图像的顶点坐标为(1,-4),且经过点(2,-2).(1)求该二次函数的解析式(2) 2020-06-27 …
已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<π2)的部分图象如图所示.(1 2020-07-20 …
二次函数y=ax2+bx+c的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C 2020-08-01 …
函数的最小值-4,且在一周期内先出现最小值,所以A=-4函数y=Asin(ωx+φ)(ω>0,|φ| 2020-11-18 …
已知,如图,函数y=-x+2的图像与x轴,y轴分别交于点a,b如图,已知一次函数y=-x+2的图像与 2021-01-10 …