早教吧作业答案频道 -->数学-->
如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.(1)求抛物线的解析式;(2)求△MCB的面积;(3)在抛物线上是否存在点P,使△PAB的
题目详情
如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.
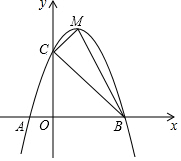
(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.

(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(1)∵A(-1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
∴
,
解方程组,得
,
故抛物线的解析式为y=-x2+4x+5;
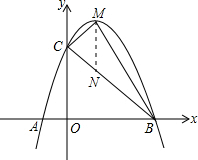 (2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=
(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=
MN•OB.
∵y=-x2+4x+5=-(x-5)(x+1)=-(x-2)2+9,
∴M(2,9),B(5,0),
由B、C两点的坐标易求得直线BC的解析式为:y=-x+5,
当x=2时,y=-2+5=3,则N(2,3),
则MN=9-3=6,
则S△MCB=
×6×5=15;
(3)在抛物线上存在点P,使△PAB的面积等于△MCB的面积.理由如下:
∵A(-1,0),B(5,0),
∴AB=6,
∵△PAB的面积=△MCB的面积,
∴
×6×|yP|=15,
∴|yP|=5,yP=±5.
当yP=5时,-x2+4x+5=5,解得x1=0,x2=4;
当yP=-5时,-x2+4x+5=-5,解得x3=2+
,x4=2-
.
故在抛物线上存在点P1(0,5),P2(4,5),P3(2+
,-5),P3(2-
,-5),使△PAB的面积等于△MCB的面积.
∴
|
解方程组,得
|
故抛物线的解析式为y=-x2+4x+5;
 (2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=
(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=| 1 |
| 2 |
∵y=-x2+4x+5=-(x-5)(x+1)=-(x-2)2+9,
∴M(2,9),B(5,0),
由B、C两点的坐标易求得直线BC的解析式为:y=-x+5,
当x=2时,y=-2+5=3,则N(2,3),
则MN=9-3=6,
则S△MCB=
| 1 |
| 2 |
(3)在抛物线上存在点P,使△PAB的面积等于△MCB的面积.理由如下:
∵A(-1,0),B(5,0),
∴AB=6,
∵△PAB的面积=△MCB的面积,
∴
| 1 |
| 2 |
∴|yP|=5,yP=±5.
当yP=5时,-x2+4x+5=5,解得x1=0,x2=4;
当yP=-5时,-x2+4x+5=-5,解得x3=2+
| 14 |
| 14 |
故在抛物线上存在点P1(0,5),P2(4,5),P3(2+
| 14 |
| 14 |
看了如图,抛物线y=ax2+bx+...的网友还看了以下:
抛物线y=x方+x的顶点在第几象限 2020-05-13 …
抛物线y=x2-x的顶点坐标是()A.(1,1)B.(0.5,1)C.(0.5,0.25)D.(0 2020-05-13 …
求顶点坐标有一个单位圆,设单位圆与x轴交于PQ两点,另有一点M在原上(异于PQ),然后PM交x=3 2020-05-13 …
已知抛物线y=x²的顶点为C,直线y=x+2与抛物线交于A、B两点,试求S△ABC 2020-05-16 …
已知二次函数y=x^2-(m^2+8)x+2(m^2+6),设抛物线顶点为A,与X轴交于B,C两点 2020-05-16 …
关于对勾函数的顶点比如y=ax+b/x的顶点坐标是什么,不要推导 2020-05-23 …
已知:如图F5—3,正比例函数y=ax的图像与反比例函数y=k/x的交于点A(3,2).1、试确定 2020-06-06 …
已知二次函数f(x)的顶点坐标为(2,-1),且图像过点(3,1)求二次函数解析式并指出单调区间当 2020-06-06 …
急求助设f(x)使R上的偶函数,当0小于等于x小于等于2时,y=x,当x大于2时,f(x)的图象是 2020-06-26 …
设函数f(x)=根3sin(x)+cos(x),角x的顶点与坐标接如题.坐标原点重合,始边与x轴非 2020-06-27 …