早教吧作业答案频道 -->数学-->
如图(1),在矩形ABCD中,将矩形折叠,使点B落在AD(含端点)上,落点记为E,这时,折痕与边BC或边CD(含端点)交于点F,然后再展开铺平,则以点B、E、F为顶点的△BEF称为矩形ABCD的“折
题目详情
如图(1),在矩形ABCD中,将矩形折叠,使点B落在AD(含端点)上,落点记为E,这时,折痕与边BC或边CD(含端点)交于点F,然后再展开铺平,则以点B、E、F为顶点的△BEF称为矩形ABCD的“折痕三角形”.
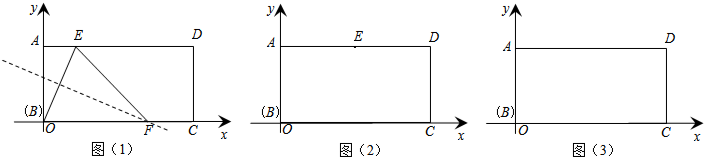
(1)如图(2),在矩形ABCD中,AB=2,BC=4,当它的“折痕△BEF”的顶点位于边AD的中点时,画出“折痕△BEF”,并求出点F的坐标;
(2)如图(3),在矩形ABCD中,AB=2,BC=4,该矩形是否存在面积最大的“折痕△BEF”?若存在,求出点E的坐标,若不存在,说明理由.

(1)如图(2),在矩形ABCD中,AB=2,BC=4,当它的“折痕△BEF”的顶点位于边AD的中点时,画出“折痕△BEF”,并求出点F的坐标;
(2)如图(3),在矩形ABCD中,AB=2,BC=4,该矩形是否存在面积最大的“折痕△BEF”?若存在,求出点E的坐标,若不存在,说明理由.
▼优质解答
答案和解析
(1)折痕△BEF如图(2)中所示,
连接BE,画BE的中垂线交BC与点F,连接EF,△BEF是矩形ABCD的一个折痕三角形.
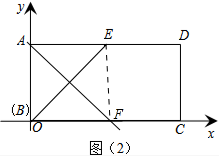
∵折痕垂直平分BE,AB=AE=2,
∴点A在BE的中垂线上,即折痕经过点A.
∴四边形ABFE为正方形.
∴BF=AB=2,
∴F(2,0).
(2)矩形ABCD存在面积最大的折痕三角形BEF,其面积为4,
理由如下:①当F在边BC上时,如图(3)中所示.
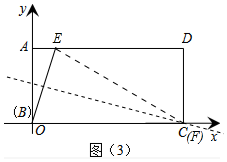
S△BEF≤
S矩形ABCD,即当F与C重合时,面积最大为4.
②当F在边CD上时,如图(4)中所示,
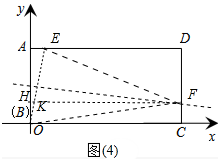
过F作FH∥BC交AB于点H,交BE于K.
∵S△EKF=
KF•AH≤
HF•AH=
S矩形AHFD,
S△BKF=
KF•BH≤
HF•BH=
S矩形BCFH,
∴S△BEF≤
S矩形ABCD=4.
即当F为CD中点时,△BEF面积最大为4.
下面求面积最大时,点E的坐标.
①当F与点C重合时,如图(3)所示.
由折叠可知CE=CB=4,
在Rt△CDE中,ED=
=2
.
∴AE=4-2
.
∴E(4-2
,2).
②当F在边DC的中点时,点E与点A重合,此时E(0,2).
综上所述,折痕△BEF的最大面积为4时,点E的坐标为E(0,2)或E(4-2
,2).
连接BE,画BE的中垂线交BC与点F,连接EF,△BEF是矩形ABCD的一个折痕三角形.

∵折痕垂直平分BE,AB=AE=2,
∴点A在BE的中垂线上,即折痕经过点A.
∴四边形ABFE为正方形.
∴BF=AB=2,
∴F(2,0).
(2)矩形ABCD存在面积最大的折痕三角形BEF,其面积为4,
理由如下:①当F在边BC上时,如图(3)中所示.

S△BEF≤
| 1 |
| 2 |
②当F在边CD上时,如图(4)中所示,

过F作FH∥BC交AB于点H,交BE于K.
∵S△EKF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S△BKF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BEF≤
| 1 |
| 2 |
即当F为CD中点时,△BEF面积最大为4.
下面求面积最大时,点E的坐标.
①当F与点C重合时,如图(3)所示.
由折叠可知CE=CB=4,
在Rt△CDE中,ED=
| CE2-CD2 |
| 3 |
∴AE=4-2
| 3 |
∴E(4-2
| 3 |
②当F在边DC的中点时,点E与点A重合,此时E(0,2).
综上所述,折痕△BEF的最大面积为4时,点E的坐标为E(0,2)或E(4-2
| 3 |
看了如图(1),在矩形ABCD中,...的网友还看了以下:
1.人们常将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,以示祈福.绿丝带重叠部分形成的图形是 2020-05-16 …
在一个函数式变形的顺序是怎样的在y=f(x)这种函数中,讲下面变换顺序排列加上绝对值关于y轴或者x 2020-05-16 …
有3×3的九宫格,通过行内平移或者列内平移,能否将其转置?具体来说,比如123456789这么一个 2020-06-10 …
如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠 2020-06-16 …
下列词组哪些是连绵词仿佛,逍遥,荒唐,婆娑,狼狈,狼藉,匍匐,阻隘,造次,望洋哪些是双声连绵词或叠 2020-06-28 …
给定下列四个命题:(1)任何一个平面图形就是一个平面;(2)平面的形状是平行四边形;(3)三角形、 2020-08-02 …
如图所示,A、B两个正方体,它们的边长之比为2:1,密度之比为4:3,先将B放在水平桌面上,再将A叠 2020-11-08 …
两个相同频率,不同强度的电磁波A与B发生干涉或叠加之后成为电磁波AB,那么A与B跟叠加或干涉后的两个 2020-11-16 …
下列命题:①书桌面是平面;②8个平面重叠起来,要比6个平面重叠起来厚;③有一个平面的长是50m,宽是 2020-12-02 …
如图所示,甲、乙两个实心正方体放在水平地面上,若将乙叠放在甲上表面中央或将甲叠放在乙上表面中央,甲、 2020-12-03 …