早教吧作业答案频道 -->数学-->
如图(1)是矩形纸片ABCD连续两次对折展开平铺后的图形,折痕分别为EF,MN,GH.(1)如图(2),连接BD,与折痕GH,EF,MN分别交于点S,O,T,求证:OE=OF;(2)如图(3),连接ET并延长交C
题目详情
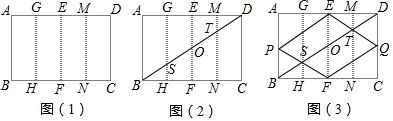
如图(1)是矩形纸片ABCD连续两次对折展开平铺后的图形,折痕分别为EF,MN,GH.
(1)如图(2),连接BD,与折痕GH,EF,MN分别交于点S,O,T,求证:OE=OF;
(2)如图(3),连接ET并延长交CD于点Q,连接FS并延长交AB于点P,连接EP,FQ.求证:四边形EPFQ是菱形;
(3)若四边形EPFQ是正方形,则矩形ABCD需满足的条件是___.
(1)如图(2),连接BD,与折痕GH,EF,MN分别交于点S,O,T,求证:OE=OF;
(2)如图(3),连接ET并延长交CD于点Q,连接FS并延长交AB于点P,连接EP,FQ.求证:四边形EPFQ是菱形;
(3)若四边形EPFQ是正方形,则矩形ABCD需满足的条件是___.

▼优质解答
答案和解析
证明:(1)如图(2),∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
由折叠得:G、E、M将AD四等分,
∴ED=BF,
∵∠EOD=∠FOB,
∴△EOD≌△FOB,
∴OE=OF;
(2)由(1)得:△EOD≌△FOB,
∴OD=OB,
连接AC,
∴A、O、C共线,
∵GT∥EO,
∴
=
=1,
∴DT=OT,
∵AE=ED,OT=DT,
∴ET∥AC,ET=
AO,
即EQ∥AC,
同理得:TQ=
OC,
∴EQ=
AC,
同理得:PF=
AC,PF∥AC,
∴PF=EQ,PF=EQ,
∴四边形EPFQ是平行四边形,
∵PF∥AC,F是BC的中点,
∴P为AB的中点,
同理得:Q为DC的中点,
∴AP=QD=
AB,
∵AE=AD,∠BAD=∠ADC=90°,
∴△APE≌△DQE,
∴PE=EQ,
∴▱EPFQ是菱形.
(3)当AB=AD时,四边形EPFQ是正方形,理由是:
∵E是AD的中点,P是AB的中点,
∴AE=
AD,AP=
AB,
∵AB=AD,
∴AP=AE,
∴△APE是等腰直角三角形,
∴∠AEP=45°,
同理∠QED=45°,
∴∠PEQ=90°,
由(2)得:四边形EPFQ是菱形,
∴四边形EPFQ是正方形;
故答案为:AB=AD.
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
由折叠得:G、E、M将AD四等分,
∴ED=BF,
∵∠EOD=∠FOB,
∴△EOD≌△FOB,
∴OE=OF;
(2)由(1)得:△EOD≌△FOB,
∴OD=OB,
连接AC,
∴A、O、C共线,
∵GT∥EO,
∴
| DG |
| EG |
| DT |
| OT |
∴DT=OT,
∵AE=ED,OT=DT,
∴ET∥AC,ET=
| 1 |
| 2 |
即EQ∥AC,
同理得:TQ=
| 1 |
| 2 |
∴EQ=
| 1 |
| 2 |
同理得:PF=
| 1 |
| 2 |
∴PF=EQ,PF=EQ,
∴四边形EPFQ是平行四边形,
∵PF∥AC,F是BC的中点,
∴P为AB的中点,
同理得:Q为DC的中点,
∴AP=QD=
| 1 |
| 2 |
∵AE=AD,∠BAD=∠ADC=90°,
∴△APE≌△DQE,
∴PE=EQ,
∴▱EPFQ是菱形.
(3)当AB=AD时,四边形EPFQ是正方形,理由是:
∵E是AD的中点,P是AB的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AD,
∴AP=AE,
∴△APE是等腰直角三角形,
∴∠AEP=45°,
同理∠QED=45°,
∴∠PEQ=90°,
由(2)得:四边形EPFQ是菱形,
∴四边形EPFQ是正方形;
故答案为:AB=AD.
看了如图(1)是矩形纸片ABCD连...的网友还看了以下:
如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种 2020-05-13 …
如图,平行四边形ABCD中,EF∥AD,MN∥AB,MN与EF交于点P,且点P在BD上.(1)图中 2020-05-15 …
如图,在平行四边形ABCD中,EF‖AD,MN‖AB,MN与EF交于点P且点 P在 BD 上(1) 2020-05-15 …
如图,在平行四边形ABCD中,MN//AB,EF//BC,EF、MN将平行四边形分成4块.如图,在 2020-05-15 …
在矩形ABCD中AB等于3,AD等于2,点EF分别在AB.DC上.AE=DF=2.再把一块直径为2 2020-05-16 …
如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.甲 2020-05-20 …
如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种 2020-06-13 …
如图,MN,EF是两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,则∠1=∠2. 2020-06-22 …
已知点a是椭圆c:x2/9+y2/t=1(T>0)的左顶点直线l:x=my+1与椭圆c相交于ef两 2020-07-30 …
如图1,将两根笔直细木板MN、EF用图钉固定并平行摆放,将一根橡皮筋拉直后用图钉分别固定在MN、E 2020-07-30 …