早教吧作业答案频道 -->数学-->
如图①,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,求证:MN=AM+CN.如图②,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上.若∠MBN=12∠ABC,试探究线段MN、AM、CN有怎样的数量
题目详情
如图①,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,求证:MN=AM+CN.
如图②,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上.若∠MBN=
∠ABC,试探究线段MN、AM、CN有怎样的数量关系?请写出猜想并给予证明.
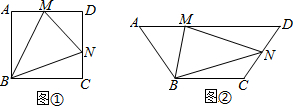
如图②,在梯形ABCD中,BC∥AD,AB=BC=CD,点M、N分别在AD、CD上.若∠MBN=
| 1 |
| 2 |

▼优质解答
答案和解析
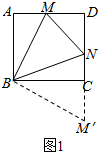 (1)证明:如图1,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
(1)证明:如图1,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,
∵∠MBN=45°=
∠ABC,
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=
∠ABC=45°,
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN;
(2) MN=AM+CN.
理由如下:
如图2,∵BC∥AD,AB=BC=CD,
∴梯形ABCD是等腰梯形,
∴∠A+∠BCD=180°,
把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,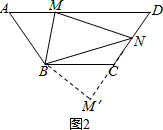
∵∠MBN=
∠ABC,
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=
∠ABC,
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN.
 (1)证明:如图1,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
(1)证明:如图1,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,
∵∠MBN=45°=
| 1 |
| 2 |
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=
| 1 |
| 2 |
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵
|
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN;
(2) MN=AM+CN.
理由如下:
如图2,∵BC∥AD,AB=BC=CD,
∴梯形ABCD是等腰梯形,
∴∠A+∠BCD=180°,
把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,

∵∠MBN=
| 1 |
| 2 |
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=
| 1 |
| 2 |
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
∵
|
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN.
看了如图①,在正方形ABCD中,点...的网友还看了以下:
若/m/=m /n/不等于n 则mn与0的关系是?A:mn>0 B:mn=0 D:mn 2020-05-14 …
矩形ABCD绕点A顺时针旋转至矩形AEFG,使B点正好落在CD上的点E处,连BE.1 求证 角BA 2020-05-16 …
如图所示,正方形ABCD边长是2,BE=CE,MN=1,线段MN的端点M、N分别在CD、AD上滑动 2020-05-17 …
设m>n>0,m^2+n^2=4mn,求m^2-n^2/mn.我做的步骤如下:原式=(m^2-n^ 2020-07-21 …
若M、N分别是△ABC边AB、AC的中点,MN与过直线BC的平面β的位置关系是()A.MN∥βB. 2020-07-22 …
若(a+m)(x+n)=x²-6x+8,则A.mn同时为负B.mn同时为正C.mn异号D.mn异号 2020-07-30 …
如图△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角 2020-07-30 …
若x的一元一次方程2x=mn+n和-2x=mn+n都是定解方程,求代数﹝式求代数式-2(m+11) 2020-07-31 …
如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是()A.M=mn 2020-11-01 …
1-mn(1-mn)-m^3n^316mn^4-m已知(19x-31)(13x-17)-(11x-2 2020-11-03 …