在梯形ABCD中,AB∥DC,AB>CD,K、M分别在AD、BC上,∠DAM=∠CBK,求证:C、D、K、M四点共圆.
思路点拨: 由∠DAM=∠CBK,易得A,B,M,K四点共圆.由此转化到相关角相等与互补,再证C,D,K,M四点共圆.
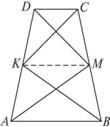
证明: 在四边形ABMK中,∵∠DAM=∠CBK,∴A,B,M,K四点共圆.
连结KM,有∠DAB=∠CMK,
∵∠DAB+∠ADC=180°,
∴∠CMK+∠KDC=180°.
故C,D,K,M四点共圆.
[一通百通] 抓住角度的相等或互补,转化为四点共圆;同样利用四点共圆,可以得到相关的角度相等.
已知平行六面体ABCD-A'B'C'D',E,F,G,H分别是棱A'D',D'C',C'C和AB的中 2020-03-31 …
提示:D-C=0A-B,A-D,D-C,D-E,E-F=1A-D,C-F=2A-B,D-E,E-F 2020-04-06 …
在0.1mol.L-1的Na2S溶液中,含有多种分子和离子,下列关系不正确的是(D) A.c(S2 2020-05-16 …
高中物理电容器在电容器中,保持开关闭合,增大d.C,U,Q怎么变化?增大S.C,U,Q怎么变化?在 2020-06-12 …
集合A有10个元素,B中有2个元素,C中有3个元素,B,C中的元素在A中都有,但B,C无公共元素, 2020-06-20 …
在平面六面体ABCD-A'B'C'D'中,E,F,G分别是A'D',D'D,D'C'的中点,请选择 2020-08-03 …
请教一下数据库里的关系题1、在关系模式R(A,B,C,D)中,有函数依赖集F={B→C,C→D,D→ 2020-11-03 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
A=>B,B=>C,C=>D,D=>E;其中=>表示左边的可以被右边的替换,根据这个逻辑可以推出来A 2021-01-07 …
常温下将氯化铵固体溶解在D2O(重水)中,下列有关水解的离子方程式或等式中正确的是()A.NH+4+ 2021-02-01 …