早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠ABC=90°,以AC为斜边向外作等腰Rt△ACD,连接BD.(1)AB=BC=2,求BD的长;(2)若AB+BC=4,求BD的长.
题目详情
如图,在Rt△ABC中,∠ABC=90°,以AC为斜边向外作等腰Rt△ACD,连接BD.
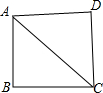
(1)AB=BC=2,求BD的长;
(2)若AB+BC=4,求BD的长.

(1)AB=BC=2,求BD的长;
(2)若AB+BC=4,求BD的长.
▼优质解答
答案和解析
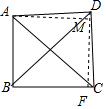 解(1)∵在Rt△ABC中,∠ABC=90°,AB=BC=2,
解(1)∵在Rt△ABC中,∠ABC=90°,AB=BC=2,
∴∠BAC=∠BCA=45°,
∵在等腰Rt△ACD,∠DAC=∠DCA=45°,
∴∠BAD=∠BCD=90°,
∴四边形ABCD是正方形,
∴BD=AC=
=2
;
(2)过D作DF⊥BC于F,过A作AM⊥DF于M,
∵∠ABC=90°,
∴∠AMD=∠DFB=90°,∠ABC=∠BFM=∠AMF=90°,
∴四边形ABFM是矩形,
∴AM=BF,AB=MF,
∵△ACD为等腰直角三角形,
∴∠ADC=90°,DA=DC,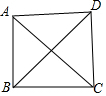
∴∠ADM+∠CDF=90°,
又∵∠AMD=90°,
∴∠ADM+∠DAM=90°,
∴∠CDF=∠DAM,
在△ADM和△DCF中
∴△ADM≌△DCF(AAS),
∴AM=DF,DM=FC,
∴DF=BF,
∵∠BFD=90°,
∴△BFD是等腰直角三角形,
∵DF+BF=DM+MF+BC-FC=AB+BC=4,
∴DF=BF=2,
∴BD=
=2
.
 解(1)∵在Rt△ABC中,∠ABC=90°,AB=BC=2,
解(1)∵在Rt△ABC中,∠ABC=90°,AB=BC=2,∴∠BAC=∠BCA=45°,
∵在等腰Rt△ACD,∠DAC=∠DCA=45°,
∴∠BAD=∠BCD=90°,
∴四边形ABCD是正方形,
∴BD=AC=
| 22+22 |
| 2 |
(2)过D作DF⊥BC于F,过A作AM⊥DF于M,
∵∠ABC=90°,
∴∠AMD=∠DFB=90°,∠ABC=∠BFM=∠AMF=90°,
∴四边形ABFM是矩形,
∴AM=BF,AB=MF,
∵△ACD为等腰直角三角形,
∴∠ADC=90°,DA=DC,

∴∠ADM+∠CDF=90°,
又∵∠AMD=90°,
∴∠ADM+∠DAM=90°,
∴∠CDF=∠DAM,
在△ADM和△DCF中
|
∴△ADM≌△DCF(AAS),
∴AM=DF,DM=FC,
∴DF=BF,
∵∠BFD=90°,
∴△BFD是等腰直角三角形,
∵DF+BF=DM+MF+BC-FC=AB+BC=4,
∴DF=BF=2,
∴BD=
| BF2+DF2 |
| 2 |
看了如图,在Rt△ABC中,∠AB...的网友还看了以下:
如图,正方形ABCD的顶点A(0,2√2),B(2√2,0),顶点C、D位于第一象限,直线l:x= 2020-06-13 …
我知道v-t图的斜率是a,但为什么x-t^2图斜率是a/2?做到用x-t^2的图像求加速度时觉得不 2020-06-27 …
下图是一列沿着x轴正方向传播的横波在t=0时刻的波形图。已知这列波的周期T=2.0s。下列说法正确 2020-07-31 …
求不定积分2、∫1/[1+√(1-x^2)]dx第二类换元法令x=sintdx=costdt∫1/ 2020-08-01 …
在对数函数y=log12x的图象上(如图),有A、B、C三点,它们的横坐标依次为t、t+2、t+4 2020-08-01 …
完成单词,并写出释义1\t-t--:2\c-mp-r-:3\-d-lt:4\-r-g-n-l:5\- 2020-12-08 …
如图,A,B,C为函数y=log1/2x的图像上的三点,它们的横坐标分别是t,t+2,t+4(t≥如 2020-12-12 …
1、在RT三角形中,角C=90度,若a=s^2-t^2,c=s^2+t^2(s>t>0),则b=?2 2020-12-25 …
下图是北京城郊年平均气温分布图。北京前门与通州相比.年平均气温的差值T最大可达[]A.1.8℃<T< 2021-01-10 …
Fluent热源设置:生热速率随温度变化,UDF怎么编写啊!!热源Qv=A*T+B*T^2+C*T^ 2021-01-12 …