早教吧作业答案频道 -->数学-->
问题情境如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.探究展示(1)证明:AM=AD+MC;(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明
题目详情
【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】
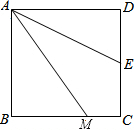
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
【探究展示】

(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
▼优质解答
答案和解析
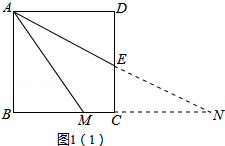 (1)证明:延长AE、BC交于点N,如图1(1),
(1)证明:延长AE、BC交于点N,如图1(1),
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴MA=MN,
在△ADE和△NCE中,
,
∴△ADE≌△NCE(AAS),
∴AD=NC,
∴MA=MN=NC+MC=AD+MC;
(2)AM=DE+BM成立,理由为:
证明:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.
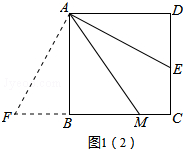 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC,
∵AF⊥AE,
∴∠FAE=90°,
∴∠FAB=90°-∠BAE=∠DAE,
在△ABF和△ADE中,
,
∴△ABF≌△ADE(ASA),
∴BF=DE,∠F=∠AED,
∵AB∥DC,
∴∠AED=∠BAE,
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM,
∴∠F=∠FAM,
∴AM=FM,
∴AM=FB+BM=DE+BM.
 (1)证明:延长AE、BC交于点N,如图1(1),
(1)证明:延长AE、BC交于点N,如图1(1),∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴MA=MN,
在△ADE和△NCE中,
|
∴△ADE≌△NCE(AAS),
∴AD=NC,
∴MA=MN=NC+MC=AD+MC;
(2)AM=DE+BM成立,理由为:
证明:过点A作AF⊥AE,交CB的延长线于点F,如图1(2)所示.
 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,∴∠BAD=∠D=∠ABC=90°,AB=AD,AB∥DC,
∵AF⊥AE,
∴∠FAE=90°,
∴∠FAB=90°-∠BAE=∠DAE,
在△ABF和△ADE中,
|
∴△ABF≌△ADE(ASA),
∴BF=DE,∠F=∠AED,
∵AB∥DC,
∴∠AED=∠BAE,
∵∠FAB=∠EAD=∠EAM,
∴∠AED=∠BAE=∠BAM+∠EAM=∠BAM+∠FAB=∠FAM,
∴∠F=∠FAM,
∴AM=FM,
∴AM=FB+BM=DE+BM.
看了问题情境如图1,四边形ABCD...的网友还看了以下:
在梯形ABCD中,AD平行CD AD=BC 点M.N为AD.BC的中点 CE垂直AB于E 若AE= 2020-05-16 …
(2011•葫芦岛一模)如图,在矩形ABCD中,AD=8,AB=6,点M是BC的中点,点P从点M出 2020-05-17 …
有一个长24厘米、宽8厘米的长方形ABCD,M点在AD边上以每秒2厘米的速度沿AD从A向D点移动; 2020-06-03 …
在△ABC中,AD是△ABC的角平分线.(1)如图1,过C作CE∥AD交BA延长线于点E,若F为C 2020-06-15 …
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=33,点M是BC的 2020-07-15 …
如图,已知正方形ABCD,AB=4,动点M、N分别从D、B两点同时出发,且都以1个单位/秒的速度匀 2020-07-19 …
如图,等腰Rt△ABD中,AB=AD,点M为边AD上一动点,点E在DA的延长线上,且AM=AE,以B 2020-11-01 …
已知正方形ABCD的边长为5,等腰直角△AEF的直角顶点E在直线BC上(不与点B,C重合),FM⊥A 2020-11-01 …
(2014•南通)如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上 2020-11-12 …
已知四边形ABCD是正方形,等腰直角△AEF的直角顶点E在直线BC上(不与点B、C重合),FM⊥AD 2021-01-02 …