早教吧作业答案频道 -->数学-->
问题情境如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.探究展示(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判
题目详情
【问题情境】
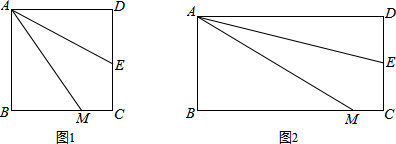
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.
【探究展示】
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
【拓展延伸】
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.

【探究展示】
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
【拓展延伸】
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
▼优质解答
答案和解析
(1)如图1,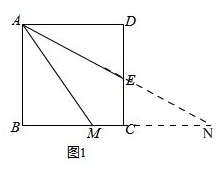 延长AE,BC相交于N,
延长AE,BC相交于N,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAE,
∴∠∠DAE=∠MAE,
∴∠ENC=∠MAE,在△ADE和△NCE中,
,
∴△ADE≌△NCE,
∴AD=CN,
∴AM=MN=NC+MC=AD+MC;
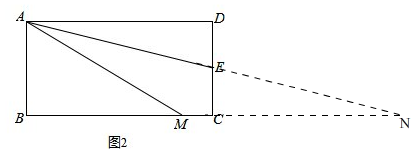
(2)结论AM=AD+CM仍然成立,
理由:如图2,
延长AE,BC相交于N,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAE,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
在△ADE和△NCE中,
,
∴△ADE≌△NCE,
∴AD=CN,
∴AM=MN=NC+MC=AD+MC;
(3)设MC=x,则BM=BC-CN=9-x,
由(2)知,AM=AD+MC=9+x,
在Rt△ABC中,AM2-BM2=AB2,
(9+x)2-(9-x)2=36,
∴x=1,
∴AM=AD+MC=10.
 延长AE,BC相交于N,
延长AE,BC相交于N,∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAE,
∴∠∠DAE=∠MAE,
∴∠ENC=∠MAE,在△ADE和△NCE中,
|
∴△ADE≌△NCE,
∴AD=CN,
∴AM=MN=NC+MC=AD+MC;

(2)结论AM=AD+CM仍然成立,
理由:如图2,
延长AE,BC相交于N,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAE,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
在△ADE和△NCE中,
|
∴△ADE≌△NCE,
∴AD=CN,
∴AM=MN=NC+MC=AD+MC;
(3)设MC=x,则BM=BC-CN=9-x,
由(2)知,AM=AD+MC=9+x,
在Rt△ABC中,AM2-BM2=AB2,
(9+x)2-(9-x)2=36,
∴x=1,
∴AM=AD+MC=10.
看了问题情境如图1,四边形ABCD...的网友还看了以下:
分解因式:(1)4a2b-6ab2+2ab(2)6(a-b)2-12(a-b)(3)x(x+y)2 2020-04-08 …
设向量a=(2sinx,cos2x),b=(2sin^2(π/4+x/2,1)(1)求|a|的最大 2020-04-27 …
已知抛物线y=(x-b)2+m-b的顶点为m与轴交于点A(x1,O),B(x2,O),且△MAB为 2020-07-12 …
已知2^m=a,32n=b,求2^(3m+10n)因为2^m=a,所以2^3m=(2^m)^3=a 2020-07-18 …
已知集合A={1,3,m},集合B={2,m的平方—m+1},且A交B={3},求实数m的值 2020-08-02 …
1.3次方根3-丨-3次方根3丨2.根号3(根号3+根号3分之1)3.(a-1)(a^4+a^3+ 2020-08-02 …
分式习题解答人教版数学书P86,1:(2).X/X-1=(3/2X-2)-2(8).(3/2)-(1 2020-10-31 …
1.若(a^n*b^m*b)³=a^9*b^15,求2^m+n的值.2.计算;a^n-5(a^n+1 2020-11-01 …
3道实数文字题~1.若m+n=10,mn=24,则m^2+n^2等于多少?2.若(a+b)^2=m, 2020-11-21 …
matlab模拟带电粒子在均匀电磁场中的运动functionydot=ddlzfun(t,y,fla 2020-12-14 …