早教吧作业答案频道 -->数学-->
若n∈N*,(an、bn∈Z).(1)求a5+b5的值;(2)求证:数列{bn}各项均为奇数.
题目详情
若n∈N * ,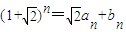 (a n 、b n ∈Z).
(a n 、b n ∈Z).
(1)求a 5 +b 5 的值;
(2)求证:数列{b n }各项均为奇数.
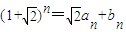 (a n 、b n ∈Z).
(a n 、b n ∈Z).(1)求a 5 +b 5 的值;
(2)求证:数列{b n }各项均为奇数.
▼优质解答
答案和解析
分析:
(1)令n=5,利用二项式定理展开,然后化简整理可求出a5与b5的值,从而求出所求;(2)利用数学归纳法证明,先奠基,然后假设假设当n=k时,然后证明当n=k+1时也成立即可.
(1)当n=5时,=[]+[]=41+故a5=29,b5=41所以a5+b5=70(2)证明:由数学归纳法(i)当n=1时,易知b1=1,为奇数;(ii)假设当n=k时,,其中bk为奇数;则当n=k+1时,=∴bk+1=bk+2ak,又ak、bk∈Z,所以2ak是偶数,由归纳假设知bk是奇数,故bk+1也是奇数综(i)(ii)可知数列{bn}各项均为奇数.
点评:
本题主要考查了二项式定理的应用,以及利用数学归纳法证明有关问题,属于中档题.
分析:
(1)令n=5,利用二项式定理展开,然后化简整理可求出a5与b5的值,从而求出所求;(2)利用数学归纳法证明,先奠基,然后假设假设当n=k时,然后证明当n=k+1时也成立即可.
(1)当n=5时,=[]+[]=41+故a5=29,b5=41所以a5+b5=70(2)证明:由数学归纳法(i)当n=1时,易知b1=1,为奇数;(ii)假设当n=k时,,其中bk为奇数;则当n=k+1时,=∴bk+1=bk+2ak,又ak、bk∈Z,所以2ak是偶数,由归纳假设知bk是奇数,故bk+1也是奇数综(i)(ii)可知数列{bn}各项均为奇数.
点评:
本题主要考查了二项式定理的应用,以及利用数学归纳法证明有关问题,属于中档题.
看了若n∈N*,(an、bn∈Z)...的网友还看了以下:
一棵树共有n个节点的数,其中所有分支节点的度均为k,则该数中叶子节点的个数为A.n(k-1)/kB 2020-04-25 …
已知函数f(x)=-2x+1,当x∈[An,Bn]时,f(x)的值域为[A(n+1),B(n+1) 2020-04-27 …
】某校为适应电化教学的需要新建阶梯教室,教室的第一排有a个座位,继续看下后面每一排都比前一排多一个 2020-05-16 …
括号内为下标:S(n)为a(n)的前n项和.a(1)=a,a(n+1)=S(n)+3^n.设b(n 2020-05-22 …
采用顺序查找法查找长度为n的线性表时,每个元素的平均查找长度为(),A.(n+1)/2B.(n-1) 2020-05-23 …
用a^n-b^n=(a-b)(a^(n-1)+a^(n-2)*b+...+ab^(n-2)+b^( 2020-07-14 …
证明:在n个正数的和为定值条件x1+x2+…+xn=a下,这n个正数的乘积x1x2…xn的最大值为 2020-07-30 …
算法时间复杂度的最高次幂项的系数很大怎么办假设时间复杂度多项式为a*n^3+b*n^2+c*n+d 2020-08-03 …
子集与推出关系课本例题:a:正整数N被5整除,p:正整数N的个位数是5.课本解题:A={n|n=5k 2020-11-28 …
自认数列NB的请进已知一个数列的递推式为ka(n-1)+d=a(n)求证它的通项公式为a(n)=a( 2020-12-10 …