如图，已知A1，A2，…，An，An+1在x轴上，且OA1=A1A2=A2A3=…=AnAn+1=1，分别过点A1，A2，…，An，An+1作x轴的垂线交直线y=x于点B1，B2，…，Bn，Bn+1，连接A1B2，B1A2，A2B3，B2A3，…，AnBn+1，BnAn+1，依次

Question

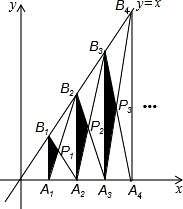
如图，已知A₁，A₂，…，A_n，A_n+1在x轴上，且OA₁=A₁A₂=A₂A₃=…=A_nA_n+1=1，分别过点A₁，A₂，…，A_n，A_n+1作x轴的垂线交直线y=x于点B₁，B₂，…，B_n，B_n+1，连接A₁B₂，B₁A₂，A₂B₃，B₂A₃，…，A_nB_n+1，B_nA_n+1，依次相交于点P₁，P₂，P₃，…，P_n，△A₁B₁P₁，△A₂B₂P₂，…，△A_nB_nP_n的面积依次为S₁，S₂，…，S_n，则S₁₌___，S_n=___．

Answer 1

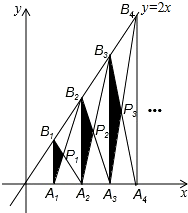∵A₁、A₂、A₃、…、A_n、A_n+1是x轴上的点，且OA₁=A₁A₂=A₂A₃=…=A_nA_n+1=1，分别过点A₁、A₂、A₃、…、A_n、A_n+1作x轴的垂线交直线y=x于点B₁、B₂、B₃、…、B_n、B_n+1，
∴依题意得：B₁（1，1），B₂（2，2），B₃（3，3），…，B_n（n，n）
∵A₁B₁∥A₂B₂，
∴△A₁B₁P₁∽△A₂B₂P₁，
∴(A1B1)/(A2B2)=(1)/(2)，
∴△A₁B₁P₁与△A₂B₂P₁对应高的比为：1：2，
∵A₁A₂=1，
∴A₁B₁边上的高为：(1)/(3)，
∴S △A1B1P1=(1)/(3)×1×(1)/(2)=(1)/(6)，
同理可得：S △A2B2P2=(2)/(5)，S△A3B3P3=(9)/(14)，
∴S_n=(n2)/(4n+2)．
故答案为(1)/(6)、(n2)/(4n+2)．