已知在直三棱柱ABC-A1B1C1中，∠BAC=120°，AB=AC=1，AA1=2，若棱AA1在正视图的投影面α内，且AB与投影面α所成角为θ（30°≤θ≤60°），设正视图的面积为m，侧视图的面积为n，当θ变化时，mn的最大

Question

已知在直三棱柱ABC-A₁B₁C₁中，∠BAC=120°，AB=AC=1，AA₁=2，若棱AA₁在正视图的投影面α内，且AB与投影面α所成角为θ（30°≤θ≤60°），设正视图的面积为m，侧视图的面积为n，当θ变化时，mn的最大值是（　　）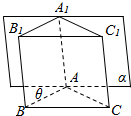

A. 2

√(3)

B. 4

C. 3

√(3)

D. 4

√(2)

Answer 1

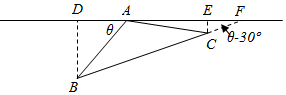
AB与投影面α所成角为θ时，平面ABC如下图所示：
∴BC=√(3)，∠ACE=60°-θ，
∴BD=ABsinθ，DA=ABcosθ，AE=ACcos（60°-θ），
ED=DA+AE=cos（60°-θ）+cosθ
故正视图的面积为m=ED×AA₁=2[cos（60°-θ）+cosθ]
侧视图的面积为n=BD×AA₁=2sinθ
∴mn=4sinθ[cos（60°-θ）+cosθ]
=4sinθ[cos60°cosθ+sinθsin60°）+cosθ]
=sin2θ+2√(3)sin²θ+2sin2θ
=3sin2θ+√(3)-√(3)cos2θ
=2√(3)sin（2θ-30°）+√(3)
∵30°≤θ≤60°
∴30°≤2θ-30°≤90°，
所以：2√(3)≤mn≤3√(3)
故得mn的最大值为3√(3)．
故选：C．